|
■（例題対比）放物線の頂点の座標
［標準形］
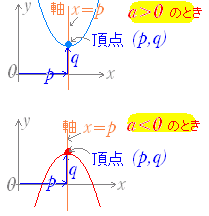
○ y=a(x−p)2+q のグラフは y=ax2 のグラフを x 軸の正の向きに p ，y 軸の正の向きに q だけ平行移動したもので，その頂点の座標は (p , q) である． 図1→ ○ ２次関数のグラフ（放物線）は左右対称になっており，この対称軸を放物線の軸という． y 軸に平行（ x 軸に垂直 ）な直線の方程式は，x=p の形で表わされるので，放物線の軸の方程式は右図のように x=1 , x=2 , x=3 などと書かれる． 図2→ 放物線の軸の方程式 x=p における p の値は頂点の x 座標に等しい．そこで，頂点の座標が分かれば軸の方程式も分かる． ［例題1］ 次の２次関数の軸の方程式と頂点の座標を求めよ． (1) y=2(x−3)2+4 （答案） 軸 x=3，頂点 (3 , 4) …（答） (2) y=3(x+4)2+5 （答案） 軸 x=−4，頂点 (−4 , 5) …（答） （x 座標の符号に注意． y=3(x−(- 4))2+5）と読む． (3) y=−4(x−5)2−6 （答案） 軸 x=5，頂点 (5 , -6) …（答） （x2 の係数 - 4 はグラフの「形」（上に凸）だけに関係しており頂点の座標には関係ない．） (4) y=  32 (x−3)2（答案） 軸 x=3，頂点 (3 , 0) …（答） （頂点が x 軸上にあるとき，このような式になる．y= 32 (x−3)2+0 と読む．）(5) y=− 23 x2+4（答案） 軸 x=0，頂点 (0 , 4) …（答） （頂点が y 軸上にあるとき，このような式になる． y=− 23 (x−0)2+4 と読む．）
［問題1］ 次の２次関数の軸の方程式と頂点の座標を求めよ．
(1) y=3(x−5)2+2
(2) y=−3(x−2)2+6
(3) y=4(x+3)2+1
|
このページのバックアップ・ページ
（グーグルブロガー版）は，こちら⇒
図1
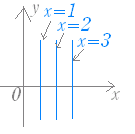  (4) y=− 12 (x− 32 )2− 54 (5) y=−5(x+3)2 (6) y=−x2−3 |
|
［展開形］
２次関数が展開形で書かれているときは，これを平方完成して標準形に直せば軸の方程式，頂点の座標が分かる． ax2+bx+c=a(x2+ ba x)+c=a{ (x+ b2a )2− b24a2 }+c=a(x+ b2a )2−a b24a2 +c=a(x+ b2a )2− b2−4ac4a ※ 実際に問題を解くときには，この公式を丸暗記するのでなく，具体的な係数に応じて平方完成の変形をするとよい．（上の結果を公式として丸暗記するのは大変だから） ［例題2］ 次の２次関数の軸の方程式と頂点の座標を求めよ． (1) y=2x2+4x+7 （答案） y=2x2+4x+7=2(x2+2x)+7 =2{ (x+1)2−1}+7 =2(x+1)2−2+7 =2(x+1)2+5 軸 x=−1，頂点 (−1 , 5) …（答）
［問題2］ 次の２次関数の軸の方程式と頂点の座標を求めよ．
(1) y=3x2−6x+4 |
(2) y=−2x2+8x (3) y=−x2−x+3 (4) y=− 12 x2+4x |