← PC梡偼暿暸
|
仭丂暘悢娭悢偺晄掕愊暘偵偮偄偰偼丆師偺棳傟偵増偭偰張棟偡傞偲暘偐傝傗偡偔側傝傑偡丏  |
|
乮侾偺徻嵶乯
丂暘巕偺師悢偑暘曣傛傝傕戝偒偄偲偒乮枖偼摍偟偄偲偒乯丆惍幃偺晹暘偲暘悢幃偺晹暘偵暘偗傞曄宍乮悢帤偱丆壖暘悢傪懷暘悢偵偡傞曄宍偵懳墳乯偼丆暘悢幃偺榓嵎傪媮傔傞偲偒丆暘悢娭悢偺僌儔僼傪彂偔偲偒丆惍悢夝傪媮傔傞偲偒丆旝暘偡傞偲偒側偳暘悢幃偵娭偡傞懡偔偺応柺偱桳岠偱偡丏偲偵偐偔丆乽暘悢幃偼仮偺嶳乿偲寛傔偰偄傞嶲峫彂傕偁傝傑偡丏 丂A亐B亖Q丒丒丒R丂偺偲偒丆乮彜亖乯惍幃晹暘偲乮梋傝亖乯暘悢幃晹暘偵暘棧偱偒傞棟桼傪丆忋偺侾偺椺傪梡偄偰夝愢偡傞偲丗 
彜偼丆暘悢偐傜摝偘傑偡丏梋傝偼丆乽巆傝乿傑偡丏
俀丆俁偺椺
乮偙偺娭學傪丆媡偵妎偊側偄傛偆偵丏乯 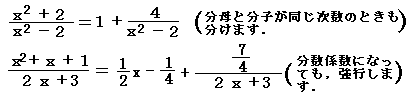 |
|
乮俀偺徻嵶乯
仜丂堦斒偵丆暘巕偺師悢偑暘曣偺師悢傛傝傕彫偝偄宍偵側偭偰偄傞偲偒丆(a,b,c偑屳偄偵堎側傞幚悢側傜偽)丂 仜丂摨條偵丂 仜丂偟偐偟丆嶲峫彂側偳偱偼丆堦斒偵暘曣偑俀忔丆俁忔側偳傪娷傫偱偄傞偲偒丗
壠棃偼丆側偤昁梫偐丠
仜丂幚偼丆
亂梫栺亃
亂椺亃偱傕 偱傕偱偒傑偡丏 偟偐偟 偺曽偑丆晄掕愊暘偺寁嶼偑妝偵側傝傑偡丏  |
|
乮俁偺徻嵶乯 埲慜丆師偺傛偆側栤戣偑弌偝傟偨偙偲偑偁傝傑偡丏 乽攚昞巻偑婘偺柺偐傜棧傟側偄傛偆偵偟側偑傜丆暘岤偄帿彂傪恾偺傛偆偵奐偄偨偲偒丆妏兤偺戝偒偝偼偄偔傜偐丏乿  崅峑偱偼丆 丂堦斒偵丆崅峑偱偼tan-1倶偲偄偆傛偆側妏搙偺昞尰曽朄偼庢傝埖偄傑偣傫偺偱丆摎偑乽媡嶰妏娭悢乿偵側傞傕偺偼弌偣傑偣傫丏偟偐偟丆tan兤=1偲側傞傛偆側妏搙偼兤亖兾乛係側偺偱丆摿掕偺抣偼弌偣傞偙偲偑偁傝傑偡丏偦偙偱乮俁乯偺宍偺栤戣偼丆乽晄掕愊暘偺栤戣偲偟偰偼弌偝側偄偑乿乽掕愊暘偺栤戣偲偟偰偼弌偡乮掕愊暘偼悢帤偱偡乯乿偲偄偆庢傝埖偄偵側傝傑偡丏 丂椺奜揑偵丆暘巕偑暘曣偺旝暘偵側偭偰偄傞栤戣偼丆抲姺愊暘偵傛傝捈偪偵夝偔偙偲偑偱偒傑偡丏 椺  |
|
乵拲乶捈慜偵PC斉偐傜擖傜傟偨応崌偼丆帺摦揮憲偱僗儅儂斉偵棃偰偄傑偡偺偱丆僽儔僂僓偺乵栠傞僉乕乶偱偼栠傟傑偣傫乮摪乆弰傝偵側傞乯丏壓婰偺儕儞僋傪巊偭偰儊僯儏乕偵栠偭偰偔偩偝偄丏
|