分数関数の不定積分

== 分数関数の不定積分 == 《解説》
■　分数関数の不定積分については，次の流れに沿って処理すると分かりやすくなります．

大きな区分

現在地と前後の項目

x^αの不定積分/分数関数の不定積分1/分数関数の不定積分2/分数関数の不定積分3/分数関数の不定積分4/不定積分の置換積分1/不定積分の置換積分2/不定積分の部分積分1/不定積分の部分積分2/多項式,分数関数,無理関数の不定積分/指数,対数関数の不定積分1/指数,対数関数の不定積分2/三角関数の不定積分1/三角関数の不定積分2/不定積分（まとめ1）/不定積分（まとめ2）/不定積分の漸化式/

（１の詳細）
　分子の次数が分母よりも大きいとき（又は等しいとき），整式の部分と分数式の部分に分ける変形（数字で，仮分数を帯分数にする変形に対応）は，分数式の和差を求めるとき，分数関数のグラフを書くとき，整数解を求めるとき，微分するときなど分数式に関する多くの場面で有効です．とにかく，「分数式は△の山」と決めている参考書もあります．
　A÷B＝Q・・・R　のとき，（商＝）整式部分と（余り＝）分数式部分に分離できる理由を，上の１の例を用いて解説すると：

商は，分数から逃げます．余りは，「残り」ます．
（この関係を，逆に覚えないように．）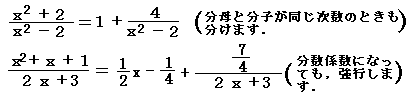

２，３の例

（２の詳細）
○　一般に，分子の次数が分母の次数よりも小さい形になっているとき，(a,b,cが互いに異なる実数ならば)　

　となる定数Ａ，Ｂはただ一通りに定まります．

○　同様に　

　となる定数Ａ，Ｂ，Ｃはただ一通りに定まります．

○　しかし，参考書などでは，一般に分母が２乗，３乗などを含んでいるとき：

　のようにおかなければならないと書かれています．（最高次のべきから，１次まで「家来を並べる」ということ．）

家来は，なぜ必要か？

○　実は，

　でもかまいません．しかし，この右辺は

　と変形できますので，ｘ²が家来を連れているのと同じことになります．また，

　も，もちろんかまいませんが，次に行う積分計算のことを考えると，

としておくと

となって，後が楽になります．

【要約】

でも

でもできます．
しかし

の方が，不定積分の計算が楽になります．

【例】

（３の詳細）
以前，次のような問題が出されたことがあります．
「背表紙が机の面から離れないようにしながら，分厚い辞書を図のように開いたとき，角θの大きさはいくらか．」

高校では，

というような角度の表現方法は扱いませんので，あえて言えば，（tanθ＝２／πという方程式の解）とでも言うべきか．角度を答えなければならないと思った受験生はさぞかし困ったことでしょう．（面接の問題）

　一般に，高校ではtan^-1ｘというような角度の表現方法は取り扱いませんので，答が「逆三角関数」になるものは出せません．しかし，tanθ=1となるような角度はθ＝π／４なので，特定の値は出せることがあります．そこで（３）の形の問題は，「不定積分の問題としては出さないが」「定積分の問題としては出す（定積分は数字です）」という取り扱いになります．
　例外的に，分子が分母の微分になっている問題は，置換積分により直ちに解くことができます．
例

←メニューに戻る

■このサイト内のGoogle検索■

△このページの先頭に戻る△【アンケート送信】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．

○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）

質問に対する回答の中学版はこの頁，高校版はこの頁にあります