== ベクトル成分の計算 ==
■[解説]
成分で表された2つのベクトル \( \displaystyle \vec{a} \)=(a1 , a2 ), \( \displaystyle \vec{a} \)=(a1 , a2 ),  \( \displaystyle \vec{b} \)=(b1 , b2 )について, \( \displaystyle \vec{b} \)=(b1 , b2 )について,
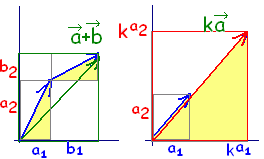
 \( \displaystyle \vec{a} \)+ \( \displaystyle \vec{a} \)+ \( \displaystyle \vec{b} \)の成分は, (a1 + b1 , a2 + b2 ) \( \displaystyle \vec{b} \)の成分は, (a1 + b1 , a2 + b2 )
 \( \displaystyle \vec{a} \)− \( \displaystyle \vec{a} \)− \( \displaystyle \vec{b} \)の成分は, (a1 − b1 , a2 − b2 ) \( \displaystyle \vec{b} \)の成分は, (a1 − b1 , a2 − b2 )
 \( \displaystyle k\vec{a} \)の成分は, (ka1 , ka2 ) \( \displaystyle k\vec{a} \)の成分は, (ka1 , ka2 )
となります。
たとえ話による解説:
男子a1人,女子a2人と男子b1人,女子b2人を合わせると,
男子a1+b1人,女子a2+b2人となり,男女数は混ざらない。
|
■[要約]
(a1 , a2 ) + (b1 , b2 ) = (a1 + b1 , a2 + b2 )
(a1 , a2 ) − (b1 , b2 ) = (a1 − b1 , a2 − b2 )
k(a1 , a2 ) = (ka1 , ka2 )
(1, 2) + (3, 4) = (4, 6)
(1, 2) − (3, 4) = (−2, −2)
3(1, 2) = (3, 6)
|

 :正答,
:正答, :誤答
:誤答