|
■[解説] △ABCにおいてA, B, Cの位置ベクトルを各々 \(\vec{a},\hspace{3px}\vec{b},\hspace{3px}\vec{c}\)とするとき, 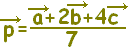 で表される点Pは, 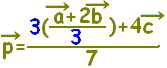 と変形することにより(割って掛ければ変わらない) ABを2:1に内分する点D()を用いて, 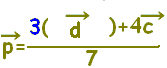 と表されます。 したがって,PはDCを4:3に内分する点となります。 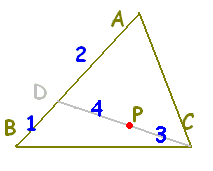
【要約】
この結果を使って,次のような三角形の面積比を答えさせる問題がよく見られます。 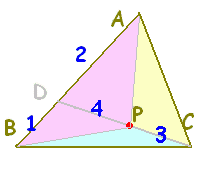
△ADP=4tとおくと、△ACP=3t
(高さが共通,底辺が4:3) △BDP=2t(△ADPの半分) △BCP=1.5t(△ACPの半分) となるから △ABP:△BCP:△CAPの面積比は,6t:1.5t:3t=12:3:6=4:1:2 (分子の係数の比:向かい側) |
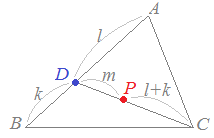
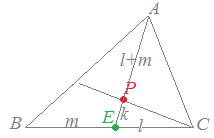

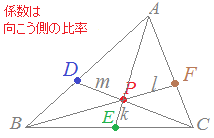

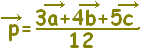 で表される点Pについて,次の空欄を埋めなさい。
で表される点Pについて,次の空欄を埋めなさい。