|
�y���̃y�[�W�̃e�[�}�z
���̃y�[�W�ł́C���̂悤�Ȗ����C���ʊ̒藝��x�N�g���i���f���j���g���ĉ������@���l���܂�.
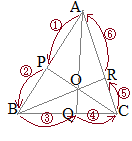
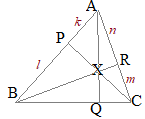 �@��ABC�ɂ����āCAB��k:l�ɓ�������_��P�CCA��m:n�ɓ�������_��R�Ƃ��CCP��BR�̌�_��X�Ƃ���D����ɁCAX�̉�����BC�ƌ����_��Q�Ƃ���D
�@��ABC�ɂ����āCAB��k:l�ɓ�������_��P�CCA��m:n�ɓ�������_��R�Ƃ��CCP��BR�̌�_��X�Ƃ���D����ɁCAX�̉�����BC�ƌ����_��Q�Ƃ���D�@���̂Ƃ��CBQ:QC, AX:XQ, BX:XR, CX:XP�͊��ɂȂ邩�H
�y�v�_�P�F���l���E�X�̒藝�z
(���l���E�X�̓M���V���̐��w��,1���I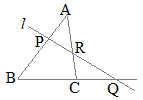 �@����l����ABC�̂R��AB, BC, CA�܂��͂��̉����ƁC���ꂼ��CP, Q, R�Ō����Ƃ��C���̎������藧�D
�@����l����ABC�̂R��AB, BC, CA�܂��͂��̉����ƁC���ꂼ��CP, Q, R�Ō����Ƃ��C���̎������藧�D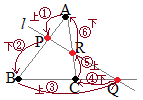 �i�����̌����j
�i�����̌����j�@�E�}�̂悤�ɁC���_A����X�^�[�g���āC��_P�܂ł̒����q�i��j�Ƃ��C���ɁC��_P���璸�_B�܂ł̒�����i���j�Ƃ���D�ȉ����l�ɕ������|���čs���āC���_A�܂Ŗ߂�����C�����̕����̐ς��P�ɂȂ�Ƃ����Ӗ� �@�E�̐}�ł́C��_Q�����ςȈʒu�ɂ���悤�Ɍ����邪�C�P�̒����ƂR��AB, BC, CA�̌�_���l����Ƃ��C���Ȃ��Ƃ��P�̌�_�͕ӂ̉�����ɗ���D �@�B�FBC→�C�FCQ�ƌ���̂ł͂Ȃ��C��̒藝�̂悤���B�FBQ→�C�FQC�Ɛ������ǂނɂ́C�@�B�I��
�y�v����Ɂz
 �ʏ�C�u���l���E�X�̒藝�v�Ƃ����ꍇ�͕��q����X�^�[�g���闬��ɂȂ��Ă���D ���ؖ������̃y�[�W |
 �@
�@ �i�����̌����j
�i�����̌����j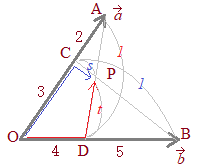 �@�E�}�̂悤��
�@�E�}�̂悤��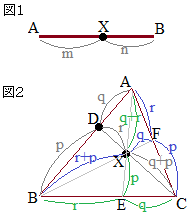 �@�E�}�P�̂悤�ɁC�Q�_
�@�E�}�P�̂悤�ɁC�Q�_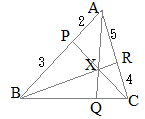 �y���P�z
�y���P�z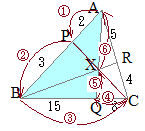 �����l���E�X�̒藝���E�}�̂悤�Ɏg����
�����l���E�X�̒藝���E�}�̂悤�Ɏg����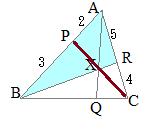 �����l���E�X�̒藝���E�}�̂悤�Ɏg����
�����l���E�X�̒藝���E�}�̂悤�Ɏg����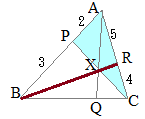 �����l���E�X�̒藝���E�}�̂悤�Ɏg����
�����l���E�X�̒藝���E�}�̂悤�Ɏg����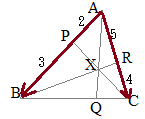 �@�E�}�̂悤�ɓ_
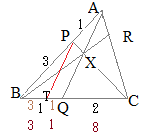
�@�E�}�̂悤�ɓ_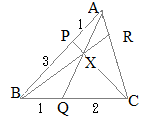 �y���Q�z
�y���Q�z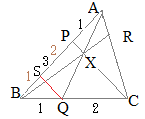
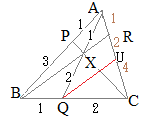
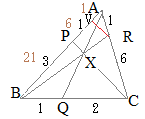
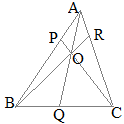
 ��ABR�ɒ���PXC�������}�`�ɑ��ă��l���E�X�̒藝��K�p�����
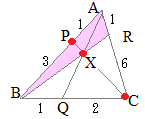
��ABR�ɒ���PXC�������}�`�ɑ��ă��l���E�X�̒藝��K�p�����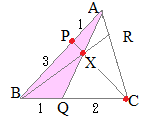 ��ABQ�ɒ���PXC�������}�`�ɑ��ă��l���E�X�̒藝��K�p�����
��ABQ�ɒ���PXC�������}�`�ɑ��ă��l���E�X�̒藝��K�p�����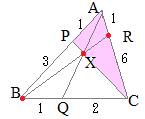 ��APC�ɒ���BXR�������}�`�ɑ��ă��l���E�X�̒藝��K�p�����
��APC�ɒ���BXR�������}�`�ɑ��ă��l���E�X�̒藝��K�p�����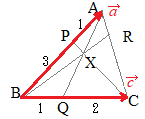 �@�E�}�ɂ����Č��_��B�ɂƂ����ʒu�x�N�g����p���āCCP��AQ�̌�_X�����߂�D
�@�E�}�ɂ����Č��_��B�ɂƂ����ʒu�x�N�g����p���āCCP��AQ�̌�_X�����߂�D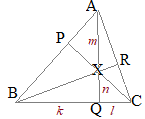 �y��ʂ�(2)�z
�y��ʂ�(2)�z