≪問題3の詳細な解答≫
数学Bのベクトルで内分比を2段階に分けて使う方法
 (そもそも)
(そもそも)
 \( \Delta ABC \)の頂点の位置ベクトルを各々 \( \Delta ABC \)の頂点の位置ベクトルを各々,\hspace{2}B(\vec{b}),\hspace{2}C(\vec{c})) \( A(\vec{a}),\hspace{2px}B(\vec{b}),\hspace{2px}C(\vec{c}) \)とするとき, \( A(\vec{a}),\hspace{2px}B(\vec{b}),\hspace{2px}C(\vec{c}) \)とするとき,
 \( \displaystyle \overrightarrow{\rm{OX}}=\frac{p\vec{a}+ q\vec{b}+ r\vec{c}}{p+ q+ r} \) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{p\vec{a}+ q\vec{b}+ r\vec{c}}{p+ q+ r} \)
) \( (p\gt 0,\hspace{2px}q\gt 0,\hspace{2px}r\gt 0) \)…(1) \( (p\gt 0,\hspace{2px}q\gt 0,\hspace{2px}r\gt 0) \)…(1)
となる点 \( X \)は \( X \)は \( \Delta ABC \)の内部の1点を表す. \( \Delta ABC \)の内部の1点を表す.
(式の見方)
例えば
 \( \displaystyle \overrightarrow{\rm{OX}}=\frac{3\vec{a}+ 4\vec{b}+ 5\vec{c}}{3+ 4+ 5} \) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{3\vec{a}+ 4\vec{b}+ 5\vec{c}}{3+ 4+ 5} \)
の分母と分子を各々2倍したとき
 \( \displaystyle \overrightarrow{\rm{OX}}=\frac{6\vec{a}+ 8\vec{b}+ 10\vec{c}}{6+ 8+ 10} \) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{6\vec{a}+ 8\vec{b}+ 10\vec{c}}{6+ 8+ 10} \)
が全く同じ点を表すことからも分かるように,(1)のp, q, rの値自体には意味はなく,p:q:rの比率に意味がある.そのため,参考書では
 \( \displaystyle \overrightarrow{\rm{OX}}=p\vec{a}+ q\vec{b}+ r\vec{c} \) \( \displaystyle \overrightarrow{\rm{OX}}=p\vec{a}+ q\vec{b}+ r\vec{c} \)
( p+q+r=1 )…(2)
の形で使うことが多い.
以下においては,p, q, rは比率だけに意味があるということを押えた上で(1)を使う.
 (理屈)
(理屈)
 \( \displaystyle \overrightarrow{\rm{OX}}=\frac{p\vec{a}+ q\vec{b}+ r\vec{c}}{p+ q+ r} \) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{p\vec{a}+ q\vec{b}+ r\vec{c}}{p+ q+ r} \)
( p>0, q>0, r>0 )…(1)
のとき
\frac{p\vec{a}%2B q\vec{b}}{p%2B q}%2b r\vec{c}}{(p%2B q)%2B r}) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{(p+ q)\dfrac{p\vec{a}+ q\vec{b}}{p+ q}+ r\vec{c}}{(p+ q)+ r} \)…(2) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{(p+ q)\dfrac{p\vec{a}+ q\vec{b}}{p+ q}+ r\vec{c}}{(p+ q)+ r} \)…(2)
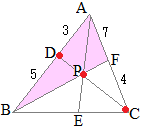
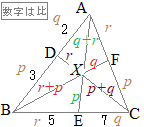
のように変形できるから,ABをq:pに内分する点をDとするとき,XはDCをr:(p+q)に内分する点になる.
同様にして
\frac{q\vec{b}%2b r\vec{c}}{q%2B r}}{p%2B(q%2B r)}) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{p\vec{a}+(q+ r)\dfrac{q\vec{b}+ r\vec{c}}{q+ r}}{p+(q+ r)} \)…(3) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{p\vec{a}+(q+ r)\dfrac{q\vec{b}+ r\vec{c}}{q+ r}}{p+(q+ r)} \)…(3)
のように変形できるから,BCをr:qに内分する点をEとするとき,XはEAをp:(q+r)に内分する点になる.
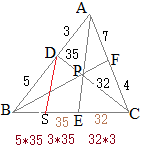
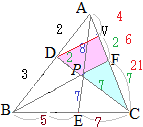
(2)の分子からp:q=3:2,(3)の分子からq:r=7:5
したがって,2と7を最小公倍数14でそろえると,p:q:r=21:14:10
 \( \displaystyle \overrightarrow{\rm{OX}}=\frac{21\vec{a}+ 14\vec{b}+ 10\vec{c}}{21+ 14+ 10} \)…(4) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{21\vec{a}+ 14\vec{b}+ 10\vec{c}}{21+ 14+ 10} \)…(4)
(問題の解き方)
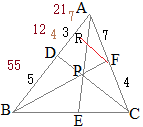
CF:FA, AX:XE, BX:XF, CX:XDをそれぞれ最も簡単な整数比で表してください.
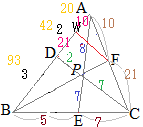
(4)より
\frac{21\vec{a}%2b 10\vec{c}}{21%2B 10}%2B 14\vec{b}}{(21%2B 10)%2B 14}) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{(21+ 10)\dfrac{21\vec{a}+ 10\vec{c}}{21+ 10}+ 14\vec{b}}{(21+ 10)+ 14} \) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{(21+ 10)\dfrac{21\vec{a}+ 10\vec{c}}{21+ 10}+ 14\vec{b}}{(21+ 10)+ 14} \)
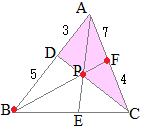
と変形できるから,Xは,「ACを10:21に内分する点F」と「B」を14:31に内分する点になる.
CF:FA=21:10…(答)
BX:XF=31:14…(答)
(4)より
\frac{14\vec{b}%2b 10\vec{c}}{14%2B 10}}{21%2B(14%2B 10)}) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{21\vec{a}+(14+ 10)\dfrac{14\vec{b}+ 10\vec{c}}{14+ 10}}{21+(14+ 10)} \) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{21\vec{a}+(14+ 10)\dfrac{14\vec{b}+ 10\vec{c}}{14+ 10}}{21+(14+ 10)} \)
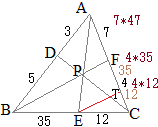
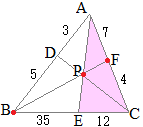
と変形できるから,Xは,「BCを10:14に内分する点E」と「A」を21:24に内分する点になる.
AX:XE=24:21=8:7…(答)
(4)より
\frac{21\vec{a}%2B 14\vec{b}}{21%2B 14}%2b 10\vec{c}}{(21%2B 14)%2B 10}) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{(21+ 14)\dfrac{21\vec{a}+ 14\vec{b}}{21+ 14}+ 10\vec{c}}{(21+ 14)+ 10} \) \( \displaystyle \overrightarrow{\rm{OX}}=\frac{(21+ 14)\dfrac{21\vec{a}+ 14\vec{b}}{21+ 14}+ 10\vec{c}}{(21+ 14)+ 10} \)
と変形できるから,Xは,「ABを14:21に内分する点D」と「C」を10:35に内分する点になる.
CX:XD=35:10=7:2…(答)
|
 【例題1】
【例題1】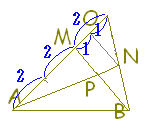 ・・(a)
・・(a)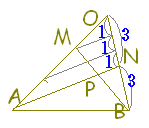 ・・(b)
・・(b)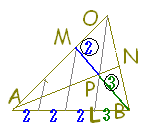
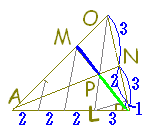
 【問題1】
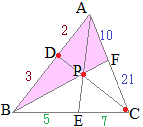
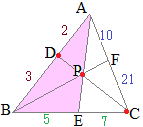
【問題1】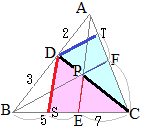 AD:DB=2:3, BE:EC=5:7のとき
AD:DB=2:3, BE:EC=5:7のとき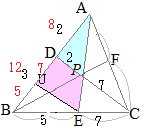
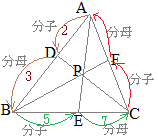
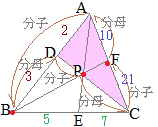

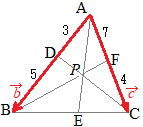
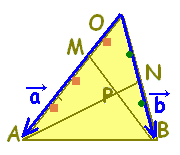
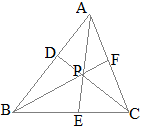
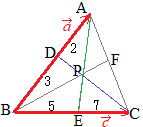 数学Bのベクトルで「2直線の交点を求める」とは,たとえば右図において原点をBにとった位置ベクトルを用いて,DCとAEの交点Pを求めるには,直線DCのベクトル方程式(1)と直線AEのベクトル方程式(2)を求め,両方を満たすベクトルをPの位置ベクトルとする.
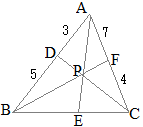
数学Bのベクトルで「2直線の交点を求める」とは,たとえば右図において原点をBにとった位置ベクトルを用いて,DCとAEの交点Pを求めるには,直線DCのベクトル方程式(1)と直線AEのベクトル方程式(2)を求め,両方を満たすベクトルをPの位置ベクトルとする.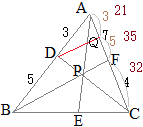 AD:DB=3:5, CF:FA=4:7のとき
AD:DB=3:5, CF:FA=4:7のとき