|
≪要点≫
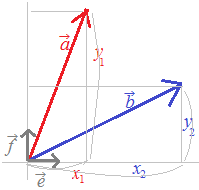
2つのベクトルが成分で表されているとき 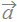 =(x1 , y1 ) , =(x1 , y1 ) , 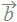 =(x2 , y2 ) の内積は =(x2 , y2 ) の内積は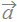 · ·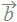 =x1x2+y1 y2 =x1x2+y1 y2
【例1】 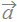 =(1 , 2 ) , =(1 , 2 ) , 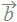 =(3 , 4 ) の内積は =(3 , 4 ) の内積は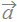 · ·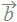 =1 · 3+2 · 4=11 =1 · 3+2 · 4=11
【例2】 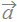 =(3 , 4 ) , =(3 , 4 ) , 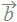 =(−5 , 7 ) の内積は =(−5 , 7 ) の内積は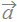 · ·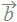 =3 · (−5)+4 · 7=13 =3 · (−5)+4 · 7=13
【例3】 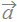 =(2 , −1 ) , =(2 , −1 ) , 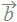 =(−3 , 0 ) の内積は =(−3 , 0 ) の内積は · · =2 · (−3)+(−1) · 0=−6 =2 · (−3)+(−1) · 0=−6
※ベクトルは2次元ですが、ベクトルの内積は単なる数になります。 3次元以上のベクトルでも同様にして、次のように成分x1, x2, …が与えられているとき、
2つのベクトルの内積は、2×4+(-3)×(-2)+1×6+5×0+…と定義されます。 ⇒ 積の和になります。 Excelのワークシート関数では = SumProduct(行1,行2) または= SumProduct(列1,列2)で内積が求められます。 ※内積の計算に当たって「掛ける相手を間違わないこと」が重要。(x成分とx成分の積+y成分とy成分の積とします) ※ベクトルの内積は 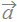 · ·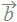 のように「ドット」で表すものとし、 のように「ドット」で表すものとし、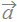 × ×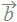 のように書いてはいけません。(×は「外積」と呼ばれる別のものを表します。) のように書いてはいけません。(×は「外積」と呼ばれる別のものを表します。) |
 (参考)
(参考)