|
◇公式の要約◇
2点 A( ) , B( ) を結ぶベクトル →AB は,→AB
=
−
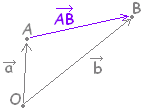
○補足説明 記号 A( ) は,関数の記号 f(x) とは無関係。 平面の座標を表わすときに,「点 A,その座標を (3 , 4) とおく」というのを A(3 , 4) と書くのと同様にして, 「点A,その位置ベクトルを とおく」というのを単に,点 A( ) と書く。 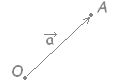 【注意】 →AB = − ではない! |
|
2点 A( ) , B( ) の中点 M の位置ベクトル は,
= ○補足説明 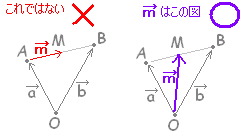 |
|
2点 A( ) , B( ) を結ぶ線分 AB m : n に内分する点 P の位置ベクトル は,
= ○補足説明 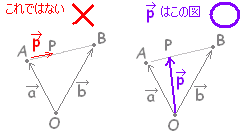 |
|
△ABC の頂点 A,B,C の位置ベクトルを各々 ,, とすると,△ABC の重心 G の位置ベクトルは,
= ○補足説明 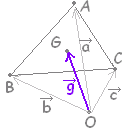 |