|
○ベクトルの和の定義から、次の図(1)のように →AB+→BC=→AC が成り立ちます。 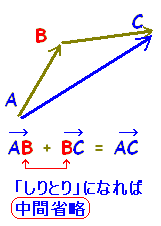
○この関係は、A,B,Cの実際の図形によらず成り立ちますので、右の図(2)の場合でも、全く同じになります。 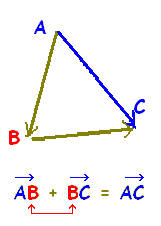
 →AB+→BA=→AA のように、終点と始点が同じになればで表します。(零ベクトルといいます。)
[要点]
2点を結んで表されたベクトルでは,「しりとり」で中間省略できる。 |
|
○ベクトルの和の定義から、次の図(1)のように →AB+→BC=→AC が成り立ちます。 
○この関係は、A,B,Cの実際の図形によらず成り立ちますので、右の図(2)の場合でも、全く同じになります。 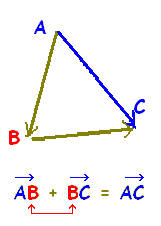
 →AB+→BA=→AA のように、終点と始点が同じになればで表します。(零ベクトルといいます。)
[要点]
2点を結んで表されたベクトルでは,「しりとり」で中間省略できる。 |
|
【例題】
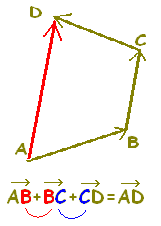
(答案)次の式を簡単にしなさい。 →AB−→DC−→AD →AB−→DC−→AD =→AB+→CD+→DA← プラスに直す =→CD+→DA+→AB← しりとり順に並べ替え =→CB← 中間を省略する
[変形のルール]
1 −→BA=→ABのように,符号がマイナス(−)のものは逆ベクトルで+に直す。 2 「しりとり」で、中間を省略できる。 |
|
【問題】 次の各式に等しいものを右から選びなさい。 ○はじめに左の問題を選び、次に対応する答を右から選びなさい。合っていれば消えます。 ○間違った場合は,答の側を連打するのではなく,問題を選び直すことから始めてください. ○間違った場合は,[解説]を読む場合でも読まない場合でも,問題を選べば解答を再開できます. ○右側にはジョーカが2枚あります。---暗算では無理ですので、計算用紙を使いましょう。  解説
解説 |
|
|