ベクトルの大きさ

...(ＰＣ版)メニューに戻る
*** 科目 ***
数Ⅰ・Ａ数Ⅱ・Ｂ数Ⅲ 高卒・大学初年度
*** 単元 ***
式と証明点と直線円軌跡と領域三角関数
指数関数対数関数微分不定積分定積分
高次方程式数列漸化式と数学的帰納法
平面ベクトル空間ベクトル確率分布

※高校数学Bの「ベクトル」について，このサイトには次の教材があります．
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください．　が現在地です．

↓ベクトルの定義
↓ベクトルの和
↓ベクトルの差
↓2点間のベクトル
↓ベクトルの実数倍
↓ベクトルの実数倍･和･差

↓ベクトルの図形への応用
↓同(2)
↓同(3)
↓同(4)
↓同(5)
↓同(6)

↓内分点の内分点
↓同(2)

↓点の存在範囲
↓同(2)

↓２直線の交点1
↓２直線の交点2
↓外心,重心,垂心,内心,オイラー線

↓ベクトル成分の計算
↓ベクトルの大きさ-現在地

↓ベクトルの内積
↓ベクトルの内積（成分）
↓ベクトルのなす角
↓|a|の変形

↓ベクトルの平行条件,垂直条件
↓一直線上にある条件

↓ベクトル方程式（内積）
↓ベクトルの公式一覧

センター試験.ベクトル.三角関数(2013年～)

== ベクトルの大きさ（長さ）==

ベクトルの大きさとは……

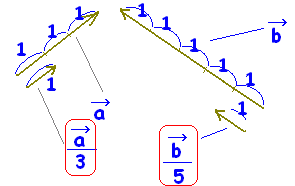
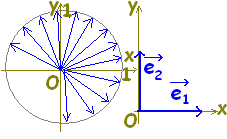
〇ベクトルは大きさと向きをもつ量です。これに対してベクトルの大きさ（長さ）は単なる１つの数です。
〇ベクトル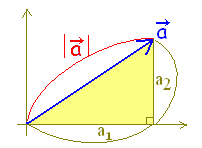

\vec{a}

の大きさ(長さ)は，絶対値記号を用いて

∣ \vec{a} ∣

で表します。

〇ベクトル

\vec{a}

の成分が

(a_{1}, a_{2})

のとき，図のように三平方の定理を用いて計算すると，

∣ \vec{a} ∣= \sqrt{a_{1}^{2} + a_{2}^{2}}

になります。
〇ベクトルの大きさは，ベクトルの始点から終点までの２点間の距離と同じです．

【例１】
　ベクトル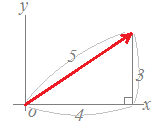

\vec{a} = (4, 3)

の大きさを求めてください．

（解答）
右図のように横の長さが4，縦の長さが3の直角三角形の斜辺の長さになるから

∣ \vec{a} ∣= \sqrt{4^{2} + 3^{2}} = \sqrt{25} = 5

…（答）

【例２】
　ベクトル

\vec{b} = (2, - 2)

の大きさを求めてください．

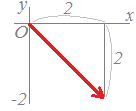（解答）
右図のように横の長さが2，縦の長さが2（ｙ座標が-2のとき長さとしては2）の直角三角形になる．
公式を使って計算するときは，負の値でも２乗すると正になるから，気にせずそのまま計算したらよい．

∣ \vec{b} ∣= \sqrt{2^{2} + (- 2)^{2}} = \sqrt{8} = 2 \sqrt{2}

…（答）

〇２点

A (a_{1}, a_{2}), B (b_{1}, b_{2})

を結ぶベクトル

\vec{A B}

の成分は，

\vec{A B} = (b_{1} - a_{1}, b_{2} - a_{2})

だから

∣ \vec{A B} ∣= \sqrt{(b_{1} - a_{1})^{2} + (b_{2} - a_{2})^{2}}

になります．これは２点間の距離

A B = \sqr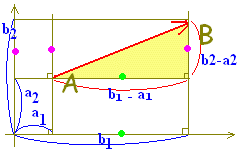t{(b_{1} - a_{1})^{2} + (b_{2} - a_{2})^{2}}

と同じです．

※ベクトルに絶対値も付けたら

∣ \vec{A B} ∣

，何も着てない裸の王様

A B

と同じ

【例３】
　２点

A (2, - 1), B (3, 2)

を結ぶベクトル

\vec{A B}

の大きさを求めてください．

（解答）

\vec{A B} = (3 - 2, 2 - (- 1)) = (1, 3)

だから

∣ \vec{A B} ∣= \sqrt{1^{2} + 3^{2}} = \sqrt{10}

…（答）

単位ベクトルとは……

〇例えば，大きさが３のベクトルを３で割ると，大きさが１のベクトルになります(向きは変わりません)。大きさが５のベクトルを５で割ると大きさ１のベクトルになります(向きは変わりません)。

〇一般に，ベクトル

\vec{a}

をその大きさ

∣ \vec{a} ∣

で割ったもの

\frac{\vec{a}}{∣ \vec{a} ∣}

は，

\vec{a}

と同じ向きで大きさ１のベクトルになります。
大きさ１のベクトルを単位ベクトルといいます。

※注意　高校には，ベクトルの割り算というものはありません。

\frac{\vec{a}}{∣ \vec{a} ∣}

は，ベクトルで割っているのでなく，記号

∣ \vec{a} ∣

は単なる数字なので，数字で割ることを表しています。数字で割ることは「ベクトルの実数倍」(大きさだけ変えて向きを変えない)で定義されています。

※向きをいろいろと考えると，大きさ1のベクトル：単位ベクトルは無数にあります。
※これに対して，ｘ軸，ｙ軸の正の向きの単位ベクトルは特に基本ベクトルと呼ばれます。基本ベクトルは，１つずつしかありません。

【例４】
　ベクトル

\vec{a} = (3, 4)

と同じ向きの単位ベクトルを求めてください．

（解答）

| \vec{a} | = \sqrt{3^{2} + 4^{2}} = 5

だから

\frac{\vec{a}}{| \vec{a} |} = \frac{\vec{a}}{5} = \frac{1}{5} (3, 4) = (\frac{3}{5}, \frac{4}{5})

…（答）
（参考）
ベクトル

\vec{a}

と「方向」が同じでも「向き」が逆のベクトルは，

(- \frac{3}{5}, - \frac{4}{5})

になります．
同一直線上にあれば「方向」が同じになりますが，あちら向きとこちら向きの違いがあります．このように「向き」が同じという指定は，「方向」が同じというよりも強い指定になります．

［要約］
〇

\vec{a} = (a_{1}, a_{2})

のとき，

∣ \vec{a} ∣= \sqrt{a_{1}^{2} + a_{2}^{2}}

〇２点

A (a_{1}, a_{2}), B (b_{1}, b_{2})

を結ぶベクトル

\vec{A B}

については，

\vec{A B} = (b_{1} - a_{1}, b_{2} - a_{2})

∣ \vec{A B} ∣= \sqrt{(b_{1} - a_{1})^{2} + (b_{2} - a_{2})^{2}}

〇

\vec{a}

と同じ向きの単位ベクトルは，

\frac{\vec{a}}{∣ \vec{a} ∣}

それぞれの問題に対応する答を下の選択肢から選びなさい。

選択肢のうちの１つをクリックすれば，採点結果と解説が出ます．解答しなければ，解説は出ません．途中の計算は，計算用紙などで行ってください．

【問題1】
(1)

A (- 1, 1), B (2, - 2)

のとき，

\vec{A B}

を求めよ．

解説やり直す

(−3, 3) (3, −3) (1, −1) (−1, 1)

ｘ成分，ｙ成分のそれぞれについて，(終点)−(始点)を計算します．

\vec{A B} = (2 - (- 1), - 2 - 1) = (3, - 3)

…（答）

→閉じる←

(2)

P (3, 0), Q (0, 3)

のとき，

\vec{P Q}

を求めよ．

解説やり直す

(−3, 3) (3, −3) (−3, −3) (3, 3)

ｘ成分，ｙ成分のそれぞれについて，(終点)−(始点)を計算します．

\vec{P Q} = (0 - 3), 3 - 0) = (- 3, 3)

…（答）

→閉じる←

【問題2】
(1)

\vec{a} = (- 2, 3)

のとき，

∣ \vec{a} ∣

を求めよ．

解説やり直す

- 1

5

2 \sqrt{2}

\sqrt{13}

\vec{a} = (a_{1}, a_{2})

のとき，

∣ \vec{a} ∣= \sqrt{a_{1}^{2} + a_{2}^{2}}

を求めます．

∣ \vec{a} ∣= \sqrt{(- 2)^{2} + 3^{2}} = \sqrt{13}

…（答）

→閉じる←

(2)

\vec{b} = (- 3, 4)

のとき，

∣ \vec{b} ∣

を求めよ．

解説やり直す

1

5

2 \sqrt{2}

\sqrt{13}

\vec{b} = (b_{1}, b_{2})

のとき，

∣ \vec{b} ∣= \sqrt{b_{1}^{2} + b_{2}^{2}}

を求めます．

∣ \vec{b} ∣= \sqrt{(- 3)^{2} + 4^{2}} = 5

…（答）

→閉じる←

(3)

A (3, 4), B (5, 6)

のとき，

∣ \vec{A B} ∣

を求めよ．

解説やり直す

1

5

2 \sqrt{2}

\sqrt{13}

A (a_{1}, a_{2}), B (b_{1}, b_{2})

に対して，

∣ \vec{A B} ∣= \sqrt{(b_{1} - a_{1})^{2} + (b_{2} - a_{2})^{2}}

を求めます．

∣ \vec{A B} ∣= \sqrt{(5 - 3)^{2} + (6 - 4)^{2}} = \sqrt{4 + 4}

= \sqrt{8} = 2 \sqrt{2}

…（答）

→閉じる←

(4)

A (- 1, 1), B (1, 2)

のとき，

∣ \vec{A B} ∣

を求めよ．

解説やり直す

5

\sqrt{5}

2 \sqrt{2}

\sqrt{13}

A (a_{1}, a_{2}), B (b_{1}, b_{2})

に対して，

∣ \vec{A B} ∣= \sqrt{(b_{1} - a_{1})^{2} + (b_{2} - a_{2})^{2}}

を求めます．

∣ \vec{A B} ∣ = \sqrt{(1 - (- 1))^{2} + (2 - 1)^{2}} = \sqrt{4 + 1} = \sqrt{5}

…（答）

→閉じる←

【問題3】
(1)

\vec{a} = (1, 1)

と同じ向きの単位ベクトルを求めよ．

解説やり直す

(\frac{1}{2}, \frac{1}{2})

(\frac{1}{2}, - \frac{1}{2})

(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})

(\frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2})

初めに

∣ \vec{a} ∣

を計算し，次に各成分をその数字で割ります．

∣ \vec{a} ∣= \sqrt{1^{2} + 1^{2}} = \sqrt{2}

\frac{\vec{a}}{∣ \vec{a} ∣} = \frac{(1, 1)}{\sqrt{2}} = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) = (\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})

…（答）

→閉じる←

(2)

\vec{b} = (- 1, 1)

と逆向きの単位ベクトルを求めよ．

解説やり直す

(\frac{1}{2}, \frac{1}{2})

(\frac{1}{2}, - \frac{1}{2})

(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})

(\frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2})

初めに

∣ \vec{b} ∣

を計算し，次に各成分をその数字で割り，さらに符号を変えます．

∣ \vec{b} ∣= \sqrt{(- 1)^{2} + 1^{2}} = \sqrt{2}

\frac{\vec{b}}{∣ \vec{b} ∣} = \frac{(- 1, 1)}{\sqrt{2}} = (- \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) = (- \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})

の符号を変えると

- \frac{\vec{b}}{∣ \vec{b} ∣} = (\frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2})

…（答）

→閉じる←

...（携帯版）メニューに戻る

...（PC版）メニューに戻る

お疲れ直しはYouTubeで（外部リンク）
∀∅ G線上のアリアバッハ ♪♫
∀∅ フーガト短調 BWV578 ♪♫

■このサイト内のGoogle検索■

△このページの先頭に戻る△【アンケート送信】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．

○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）

質問に対する回答の中学版はこの頁，高校版はこの頁にあります