== 多項式・有理関数・無理関数の不定積分 ==
■《基本公式》
(ア) α≠−1のとき
 \( \displaystyle \int x^{\alpha} dx=\frac{1}{\alpha +1}x^{\alpha + 1}+ C \) \( \displaystyle \int x^{\alpha} dx=\frac{1}{\alpha +1}x^{\alpha + 1}+ C \)
この頁の下の問題に多く登場するように αが分数(有理数)のときは,無理関数(累乗根)の積分になります.
【例】
 \( \displaystyle \int \sqrt{x}dx=\int x^{\frac{1}{2}} dx=\frac{1}{\frac{3}{2}}x^{\frac{3}{2}}+ C \) \( \displaystyle \int \sqrt{x}dx=\int x^{\frac{1}{2}} dx=\frac{1}{\frac{3}{2}}x^{\frac{3}{2}}+ C \)
(イ) α=−1のとき
 \( \displaystyle \int x^{-1} dx=\int \frac{1}{x}dx=\log |x|+ C \) \( \displaystyle \int x^{-1} dx=\int \frac{1}{x}dx=\log |x|+ C \)
α=−1のときだけは例外です・・・これが重要
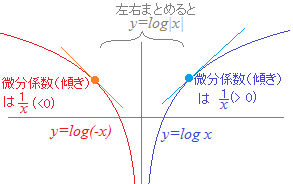
なお, \apos =\frac{1}{x}&chco=aa4422) \( \displaystyle (\log x)' =\frac{1}{x} \) \( \displaystyle (\log x)' =\frac{1}{x} \)…(*1)ですが
)\apos =\frac{1}{x}&chco=aa4422) \( \displaystyle (\log (-x))' =\frac{1}{x} \) \( \displaystyle (\log (-x))' =\frac{1}{x} \)…(*2)も成り立ちますので,2つまとめて
\apos =\frac{1}{x}&chco=aa4422) \( \displaystyle (\log |x|)' =\frac{1}{x} \) \( \displaystyle (\log |x|)' =\frac{1}{x} \)
すなわち
 \( \displaystyle \int x^{-1} dx=\int \frac{1}{x}dx=\log |x|+ C \) \( \displaystyle \int x^{-1} dx=\int \frac{1}{x}dx=\log |x|+ C \)
と書くことができます.
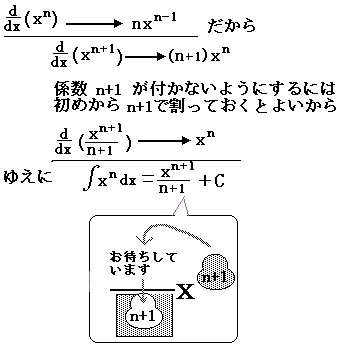
(ア)←
xαを微分すると次数が1次下がります.
|
(イ)←
1次(x1)の微分は0次(定数項)です.
しかし,0次(定数項)の微分だけは0次なので,
微分して-1次となるものが多項式や有理関数の中にはありません.
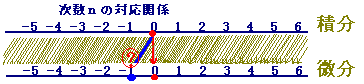
ここで,微分してx-1となる場所を埋めているのが,対数関数 log|x|です.
|