|
→ 携帯用は別頁
【公式】
○媒介変数表示で表される曲線x=f(t) , y=g(t)の区間α≦t≦βにおける曲線の長さは ○x ,y直交座標で表される曲線y=f(x)の区間a≦x≦bにおける曲線の長さは ○極座標で表される曲線r=f(θ)の区間α≦θ≦βにおける曲線の長さは ※極座標で表される曲線の長さの公式は,高校向けの教科書や参考書には掲載されていないが,媒介変数表示で表される曲線と解釈すれば解ける.([→例]) |
(解説)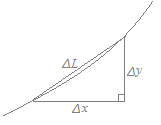 したがって |
|
○x ,y直交座標ではx=tとおけば上記の公式が得られる.
図で言えば
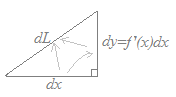 |
○極座標でr=f(θ)のとき,媒介変数をθに選べば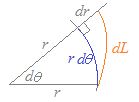 極座標でrが一定ならば,弧の長さはdL=rdθで求められるが,一般にはrも変化する.
極座標でrが一定ならば,弧の長さはdL=rdθで求められるが,一般にはrも変化する.そこで, |
|
■以下の問題を全部を解く必要はない.できそうな,または,気になる問題をそれぞれの○から2題ほど解けばよい.
○媒介変数表示
|
○x ,y直交座標
|
○極座標
|
|
|
(1-1) サイクロイドの長さ
(答案)a>0 , 0≦t≦2π  だから したがって |
(1-2) アステロイド(
a>0 , 0≦θ≦2π 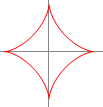 x軸についても,y軸についても対称となるから,
x軸についても,y軸についても対称となるから,の区間の長さを4倍すればよい. だから だから |
 (1.3)
(1.3) 0≦t≦1 だから |
(1.4)
0≦t≦1 (首都東京大学2005年)
 (答案)
(答案)だから |
|
○x ,y直交座標
(2.1) 懸垂曲線(カテナリ-)
0≦x≦1 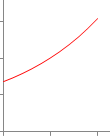 (参考)
(参考)の曲線は懸垂曲線(カテナリー)と呼ばれ,均質なロープを吊るすとこの曲線ができる.ここではa=1の簡単な場合を扱う. だから したがって |
(2.2)
(答案)0≦x≦1 だから したがって |
|
○極座標
(3.1)心臓形(カージオイド)
(答案)a>0 , 0≦θ≦2π ところで,三角関数の2倍角公式により だから したがって ここで x<0のとき に注意すると (1) 0≦θ≦πのとき (2) π≦θ≦2πのとき
グラフからx軸に関して(上下に)対称であることを考えると,下半分も同じ長さになることが使えるが,単純に計算で示すには次のようにやればよい.
(1)(2)で求めた上半分の長さ |
(参考)
極方程式r=1+cosθ (0≦θ≦π)で表される曲線の長さを求めよ. (京都大学2009年)
→ 上記の答案でa=1, 0≦θ≦πとすると,L1=4…(答)[別解]・・・「高校では極座標の曲線の長さの公式は習わない」ことを前提にすると,これを回避する方法があるはず
x=rcosθ=(1+cosθ)cosθ
y=rsinθ=(1+cosθ)sinθ として,媒介変数表示の場合の曲線の長さを求めるとよい.
(∵)
だから 以下の記述は上の答案と同様 0≦θ≦πのとき |
|
(3.2) 半円
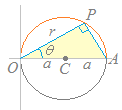 円周角の定理を思い出すと,直径の上に立つ円周角は90°になるから,直径2aにcosθを掛けた2acosθ=OPとなればPは円周上にある.
円周角の定理を思い出すと,直径の上に立つ円周角は90°になるから,直径2aにcosθを掛けた2acosθ=OPとなればPは円周上にある.したがって,この問題の結果は小学校以来学んでいる半円の長さπaになるはずであるが,これを極座標での曲線の長さの計算で確かめることになる. だから |
(3.3) 対数螺旋(等角螺旋)
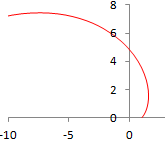 (参考)
(参考)ただし,蚊取り線香やアナログレコードのように線が等間隔に並んでいるものはアルキメデスの螺旋と呼ばれる別の渦巻きになる この問題ではa=1 , b=1の場合を扱っている だから |
|
(3.4)
(答案)関数 の長さを |
(参考1) になりますが,この「公式」を覚えるのは大変ですし,高校生が覚える必要もないでしょう.また,三角関数を経由して置換積分で求める計算をすると曲線の長さを求める問題よりも積分の方にほとんどの時間を取られてしまいます. ここでは,定積分で定義される関数を利用して問題を簡潔にしました. 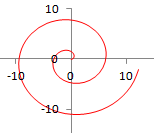 (参考2)
(参考2)アルキメデスの螺旋
r1=aθ
このような図形は,蚊取り線香やアナログレコードに見られます.r2=a(θ+2π)=aθ+2πa 右図は |
|
問題次の曲線の長さを求めてください. 正しいと思う選択肢をクリックすると,採点結果と解説が表示されます.(選択肢をクリックしなければ,解説も出ません.) 2 4 π 2π 4π
(上記の範囲では (参考) この問題は,x , y座標で与えられた方程式から曲線の長さを求める問題なので,上記のように答えてもらえばOKです. 図形的には,円x2+y2=4のうちのx≧0 , y≧0の部分なので,半径2の円のうちの第1象限の部分の長さ:2π×2÷4=πになります. |
2
4
π
2π
4π
[高校の範囲で解いた場合]
x=rcosθ=2sinθcosθ=sin2θ
として,媒介変数表示の場合の曲線の長さを求めるとよい.y=rsinθ=2sinθsinθ=1−cos2θ
(∵)cos2θ=1−2sin2より
2sin2θ=1+cos2θ |
|
|
ここで三角関数の2倍角公式により だから また三角関数の相互関係から (2)(3)を(1)に代入すると だから [高校の範囲で解いた場合]
x=rcosθ=(1+sinθ)cosθ=cosθ+sinθcosθ
として,媒介変数表示の場合の曲線の長さを求めるとよい.y=rsinθ=(1+sinθ)sinθ=sinθ+sin2θ となり(1)以下同様になる. (参考) 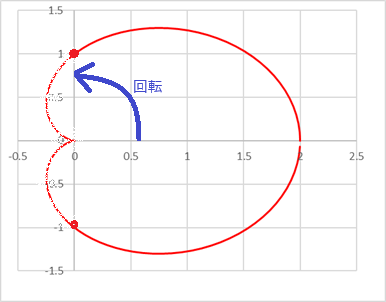
だから,このグラフはカージオイド カージオイド |
|
|
だから [高校の範囲で解いた場合]
x=rcosθ=2
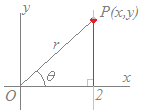 (参考)
(参考)そのうちで, |
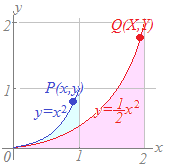 (参考2)
(参考2)
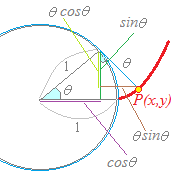 (参考)
(参考)