|
■閉曲線で囲まれた図形の面積2…(媒介変数表示)
【例1】
(解答)x=t2−1 , y=−t2+2t+3とx軸とで囲まれた図形の面積を求めてください. [曲線の概形を描く] (1) tの変化に対応したxの増減を調べる.
=2t
=−2t+2=−2(t−1)
y=−(t+1)(t−3)=0 → t=−1, 3 → x=0, 8
(4) tの変化に対応した曲線の動き調べる.
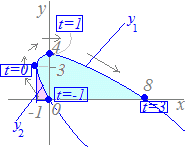 続く→
|
→続き [ 置換積分により変数をtに直して計算する] S=y1 dx−y2 dx =(−t2+2t+3)2t dt−(−t2+2t+3)2t dt 
≪(*)の式でt=0 (x=−1)の区切りを省略してしまったら,
面積が引き算になる話はどうなってしまうのか??≫ (−t2+2t+3)2t dtでピンクの図形の面積を表します だから (−t2+2t+3)2t dt=−(−t2+2t+3)2t dt が面積の引き算を表すようになるのです. 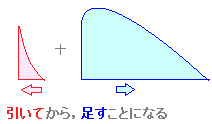 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
【例2】
(解答)x=10−t2 , y=−t2+2t+8とx軸とで囲まれた図形の面積を求めてください. [曲線の概形を描く] (1) tの変化に対応したxの増減を調べる.
=−2t
=−2t+2=−2(t−1)
y=−(t+2)(t−4)=0 → t=−2, 4 → x=6, −6
(4) tの変化に対応した曲線の動き調べる.
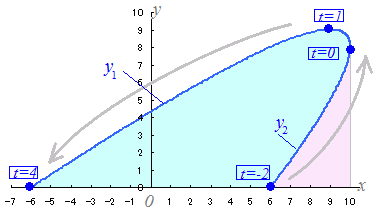 続く→
|
→続き [ 置換積分により変数をtに直して計算する] S=y1 dx−y2 dx =(−t2+2t+8)(−2t)dt−(−t2+2t+8)(−2t)dt =(−t2+2t+8)(−2t)dt …(*) =2(−t2+2t+8)tdt =2(−t3+2t2+8t)dt =2−+t3+4t2=……=72
≪繰り返しになるが(*)の式でt=0 (x=10)の区切りを省略してしまったら,面積が引き算になる話はどうなってしまうのか??≫
(−t2+2t+8)(−2t)dt でピンクの図形の面積を表すので +(−t2+2t+8)(−2t)dt が面積の引き算を表すようになるのです.  |
||||||||||||||||||||||||||||||||||||||||||||||||
|
【例3】
(解答)x=t2−2t−3 , y=t2−4tとx軸とで囲まれた図形の面積を求めてください. [曲線の概形を描く] (1) tの変化に対応したxの増減を調べる.
=2(t−1)
=2t−4=2(t−2)
y=t(t−4)=0 → t=0, 4 → x=−3, 5
(4) tの変化に対応した曲線の動き調べる.
x軸よりも下にあるので,面積は(−y)dxの形で計算します. 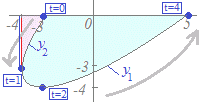 続く→
|
→続き [ 置換積分により変数をtに直して計算する] S=(−t2+4t)(2t−2)dt−(−t2+4t)(2t−2)dt =(−t2+4t)(2t−2)dt+(−t2+4t)(2t−2)dt =(−t2+4t)(2t−2)dt =2(−t2+4t)(t−1)dt =2(−t3+5t2−4t)dt =2−+t3−2t2=……= |
||||||||||||||||||||||||||||||||||||||||||||||||
|
【問題1】x=t2 , y=−t2−2t+3とx軸とで囲まれる図形について,各々正しいものを選んでください.
(1)このグラフとx軸との交点の(x)座標はHELP −3, 1 −1 , 3 1 , 9 −1 , −9 |
y=−t2−2t+3=−(t+3)(t−1)=0 より t=−3 , 1 これをx=t2に代入すると x=9 , 1 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
(2)曲線の向きについて ア) −3<t<−1の範囲でtが増加するとき HELP 
|
=2t , =−2(t+1)だから
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
イ) t=−1のとき HELP 
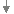
|
=2t , =−2(t+1)だから
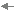
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
ウ) −1<t<0の範囲でtが増加するとき HELP 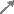
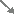
|
=2t , =−2(t+1)だから
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
エ) t=0のとき HELP 
|
=2t , =−2(t+1)だから
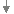
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
オ) 0<t<1の範囲でtが増加するとき HELP 
|
=2t , =−2(t+1)だから
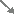
|
||||||||||||||||||||||||||||||||||||||||||||||||
(6)図のように曲線のうちで上にある部分をy1,下にある部分をy2で表すとき,この曲線とx軸とで囲まれた図形を表す式は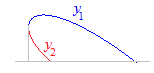 y1 dx−y2 dx y1 dx−y2 dx y1 dx−y2 dx y1 dx−y2 dx |
積分変数がxのときは,積分区間はxの値の範囲とします. y1 dx−y2 dx | ||||||||||||||||||||||||||||||||||||||||||||||||
|
(7)(6)の結果を積分変数をtにして書き換えると,次のどの式になりますか. HELP (−t2−2t+3)dt−(−t2−2t+3)dt (−t2−2t+3)dt−(−t2−2t+3)dt (−t2−2t+3)2t dt−(−t2−2t+3)2t dt (−t2−2t+3)2t dt−(−t2−2t+3)2t dt |
被積分関数について y=−t2−2t+3 積分変数について dx=2t dt 積分区間について
のように各々変換すると, (−t2−2t+3)2t dt−(−t2−2t+3)2t dt |
||||||||||||||||||||||||||||||||||||||||||||||||
|
(8)面積は,次のどの値になりますか. HELP |
2(−t2−2t+3)t dt=2(−t3−2t2+3t)dt =2−−t3+t2 =……= | ||||||||||||||||||||||||||||||||||||||||||||||||
|
【問題2】x=t2 , y=t2+t−2とx軸とで囲まれる図形の面積を求めてください
HELP=2t , =−2(t+1)だから
|
x軸よりも下にあることに注意すると S=(−y1)dx−(−y2)dx =(−t2−t+2)2t dt−(−t2−t+2)2t dt =(−t2−t+2)2t dt+(−t2−t+2)2t dt =(−t2−t+2)2t dt =2(−t3−t2+2t)dt =2−−t3+t2=……= |