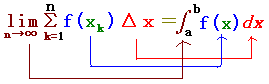=== limΣ=∫(区分求積法の入試問題)===
■ 数列の和の極限を定積分に直すには,次のような図を考えます.
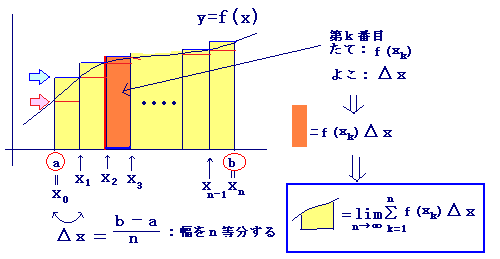
(公式)
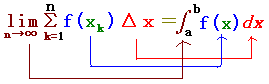
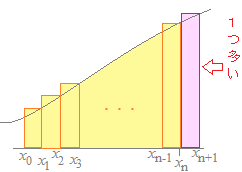
上の図において,青の矢印で示したように,各々の短冊の右肩がグラフ上にあるようにしてできた短冊の面積を全部足すと,次の公式になります.
\Delta x=\int_a^bf(x)dx\]&chco=0000ff) \( \displaystyle \lim_{n\rightarrow \infty}\sum_{k=1}^nf(x_k)\Delta x=\int_a^bf(x)dx \)…(A) \( \displaystyle \lim_{n\rightarrow \infty}\sum_{k=1}^nf(x_k)\Delta x=\int_a^bf(x)dx \)…(A)
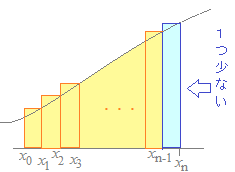
上の図において,赤の矢印で示したように,各々の短冊の左肩がグラフ上にあるようにしてできた短冊の面積を全部足すと,次の公式になります.
\Delta x=\int_a^bf(x)dx\]&chco=ff0000) \( \displaystyle \lim_{n\rightarrow \infty}\sum_{k=0}^{n-1}f(x_k)\Delta x=\int_a^bf(x)dx \)…(B) \( \displaystyle \lim_{n\rightarrow \infty}\sum_{k=0}^{n-1}f(x_k)\Delta x=\int_a^bf(x)dx \)…(B)
区分求積法によって面積を求めるときに,上の図のような単調増加関数の例で考えると,(A)は実際よりも少しずつ大きな短冊を集めたものになり,(B)は実際よりも少しずつ小さな短冊を集めたものになりますが,
 \( \displaystyle \lim_{n\rightarrow \infty},\hspace{10px}\lim_{\Delta x\rightarrow 0} \) \( \displaystyle \lim_{n\rightarrow \infty},\hspace{10px}\lim_{\Delta x\rightarrow 0} \)
のときに(A)と(B)が同じ値に収束したら,その値を図形の面積と 定義します.(単調減少関数であっても,増加区間と減少区間の両方があっても(A)(B)が一致したらそれを面積の定義とする.)
したがって,(A)と(B)は等しいと言えます.(これらが等しくなければ,面積は定義されないから)
上の図において,n個の短冊は(植木算の仕組みで)n+1本の線で区切られています.
 \( \displaystyle x_0,\hspace{5px}x_1,\hspace{5px}x_2,\hspace{5px}x_3,\hspace{5px}\cdots x_{n-1},\hspace{5px}x_n \) \( \displaystyle x_0,\hspace{5px}x_1,\hspace{5px}x_2,\hspace{5px}x_3,\hspace{5px}\cdots x_{n-1},\hspace{5px}x_n \)
のうちの
 \( \displaystyle x_1,\hspace{5px}x_2,\hspace{5px}x_3,\hspace{5px}\cdots x_{n-1},\hspace{5px}x_n \) \( \displaystyle x_1,\hspace{5px}x_2,\hspace{5px}x_3,\hspace{5px}\cdots x_{n-1},\hspace{5px}x_n \)
のn個を使う・・・(初項は \( \displaystyle x_1 \)のy座標を使う:各短冊の右肩が \( \displaystyle x_1 \)のy座標を使う:各短冊の右肩が) \( \displaystyle f(x) \)のグラフ上にある)・・・のが(A)で \( \displaystyle f(x) \)のグラフ上にある)・・・のが(A)で
 \( \displaystyle x_0,\hspace{5px}x_1,\hspace{5px}x_2,\hspace{5px}x_3,\hspace{5px}\cdots x_{n-1} \) \( \displaystyle x_0,\hspace{5px}x_1,\hspace{5px}x_2,\hspace{5px}x_3,\hspace{5px}\cdots x_{n-1} \)
のn個を使う・・・(初項は \( \displaystyle x_0 \)のy座標を使う:各短冊の左肩が \( \displaystyle x_0 \)のy座標を使う:各短冊の左肩が) \( \displaystyle f(x) \)のグラフ上にある)・・・のが(B)です. \( \displaystyle f(x) \)のグラフ上にある)・・・のが(B)です.
(A)の式では,Σ記号には積分区間の端になるべき値 \( \displaystyle x_0 \)が入っていませんが,これを求めるためには \( \displaystyle x_0 \)が入っていませんが,これを求めるためには \( \displaystyle a=x_0 \)を計算しなければなりません. \( \displaystyle a=x_0 \)を計算しなければなりません.
逆に,(B)の式でも,Σ記号には積分区間の端になるべき値 \( \displaystyle x_n \)が入っていませんが,これを求めるためには \( \displaystyle x_n \)が入っていませんが,これを求めるためには \( \displaystyle b=x_n \)を計算しなければなりません. \( \displaystyle b=x_n \)を計算しなければなりません.
■ この公式を使うには,「各部品」を正確に対応させることが大切です.(初めは,大変難しいものです.)
<要点>
[1]
まず,  \( \displaystyle \Delta x \) \( \displaystyle \Delta x \)(通常は  \( \displaystyle \frac{1}{n} \) \( \displaystyle \frac{1}{n} \))を分離すること
→ これが  \( \displaystyle dx \) \( \displaystyle dx \)になります.
(Σ記号の初項から末項までの項数 n個の等分となっている)
[2]
 \( \displaystyle x_k \) \( \displaystyle x_k \)を決める→ ) \( \displaystyle f(x_k) \) \( \displaystyle f(x_k) \)を決める→ ) \( \displaystyle f(x) \) \( \displaystyle f(x) \)を決める.
[3]
 \( \displaystyle \lim\sum\rightarrow \int \) \( \displaystyle \lim\sum\rightarrow \int \)とします.
[4]
 \( \displaystyle x_0=a,\hspace{5px}x_n=b \) \( \displaystyle x_0=a,\hspace{5px}x_n=b \)とします.(  \( \displaystyle b-a=1 \) \( \displaystyle b-a=1 \)でないなら, [1]の段階で  \( \displaystyle \Delta x \) \( \displaystyle \Delta x \)を調整します.)
※なお,数列の和 ) \( \displaystyle \sum_{k=1}^n f(x_k) \) \( \displaystyle \sum_{k=1}^n f(x_k) \)が求められるとは限らないことに注意.
数列の和 ) \( \displaystyle \sum_{k=1}^n f(x_k) \) \( \displaystyle \sum_{k=1}^n f(x_k) \)は求められない場合でも,数列の和の極限 ) \( \displaystyle \lim\sum_{k=1}^n f(x_k) \) \( \displaystyle \lim\sum_{k=1}^n f(x_k) \)は「定積分」だから計算できるのです.
極限  \( \displaystyle \lim_{n\rightarrow \infty}\frac{1}{n}\sum_{k=1}^n\cos\frac{k\pi}{3n} \) \( \displaystyle \lim_{n\rightarrow \infty}\frac{1}{n}\sum_{k=1}^n\cos\frac{k\pi}{3n} \)を求めよ.
(茨城大2014年度)
(解説)
[1] まず, \( \displaystyle \frac{1}{n} \)を分離する.(この問題では初めからそうなっている) \( \displaystyle \frac{1}{n} \)を分離する.(この問題では初めからそうなっている)
\frac{1}{n}\]) \( \displaystyle \lim_{n\rightarrow \infty}\sum_{k=1}^n\Bigl(\cos\frac{k\pi}{3n}\Bigr)\frac{1}{n} \) \( \displaystyle \lim_{n\rightarrow \infty}\sum_{k=1}^n\Bigl(\cos\frac{k\pi}{3n}\Bigr)\frac{1}{n} \)
[2]  \( \displaystyle x_k \)を決める→ \( \displaystyle x_k \)を決める→) \( \displaystyle f(x_k) \)を決める→ \( \displaystyle f(x_k) \)を決める→) \( \displaystyle f(x) \)を決める. \( \displaystyle f(x) \)を決める.
 \( \displaystyle x_k=\frac{k}{n} \) \( \displaystyle x_k=\frac{k}{n} \)
=\cos\frac{\pi}{3}x_k) \( \displaystyle f(x_k)=\cos\frac{\pi}{3}x_k \) \( \displaystyle f(x_k)=\cos\frac{\pi}{3}x_k \)
=\cos\frac{\pi}{3}x) \( \displaystyle f(x)=\cos\frac{\pi}{3}x \) \( \displaystyle f(x)=\cos\frac{\pi}{3}x \)
とおく.
[3]  \( \displaystyle \lim\sum\rightarrow \int \)とする. \( \displaystyle \lim\sum\rightarrow \int \)とする.
 \( \displaystyle \int\cos\frac{\pi}{3}xdx \) \( \displaystyle \int\cos\frac{\pi}{3}xdx \)
[4] \( \displaystyle x_0=a,\hspace{5px}x_n=b \)とします.( \( \displaystyle x_0=a,\hspace{5px}x_n=b \)とします.( \( \displaystyle b-a=1 \)でないなら,[1]の段階で \( \displaystyle b-a=1 \)でないなら,[1]の段階で \( \displaystyle \Delta x \)を調整します.) \( \displaystyle \Delta x \)を調整します.)
 \( \displaystyle x_0=\frac{0}{n}=0,\hspace{5px}x_n=\frac{n}{n}=1 \) \( \displaystyle x_0=\frac{0}{n}=0,\hspace{5px}x_n=\frac{n}{n}=1 \)
(区間の幅が 1 だから,[1]において \( \displaystyle \frac{1}{n} \)としたこととつじつまが合う) \( \displaystyle \frac{1}{n} \)としたこととつじつまが合う)
以上から
 \( \displaystyle \int_0^1\cos\frac{\pi}{3}xdx \) \( \displaystyle \int_0^1\cos\frac{\pi}{3}xdx \)
後は,この定積分を計算すればよい.
 \( \displaystyle \int_0^1\cos\frac{\pi}{3}xdx=\Big[\frac{3}{\pi}\sin\frac{\pi}{3}x\Big]_0^1 \) \( \displaystyle \int_0^1\cos\frac{\pi}{3}xdx=\Big[\frac{3}{\pi}\sin\frac{\pi}{3}x\Big]_0^1 \)
=\frac{3}{\pi}\cdot\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2\pi}) \( \displaystyle =\frac{3}{\pi}(\sin\frac{\pi}{3}-0)=\frac{3}{\pi}\cdot\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2\pi} \)…(答) \( \displaystyle =\frac{3}{\pi}(\sin\frac{\pi}{3}-0)=\frac{3}{\pi}\cdot\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2\pi} \)…(答)
右上に続く→
|
[4]に関連して: \( \displaystyle x_k \)を主役として,次のように見直してみると全体の有機的なつながりについて何かつかめる事があると思う. \( \displaystyle x_k \)を主役として,次のように見直してみると全体の有機的なつながりについて何かつかめる事があると思う.
\frac{1}{n}\]&chco=aa4422) \( \displaystyle \lim_{n\rightarrow \infty}\sum_{k=1}^n\Bigl(\cos\frac{k\pi}{3n}\Bigr)\frac{1}{n} \) \( \displaystyle \lim_{n\rightarrow \infty}\sum_{k=1}^n\Bigl(\cos\frac{k\pi}{3n}\Bigr)\frac{1}{n} \)
からスタートして,もし
=\cos x&chco=aa4422) \( \displaystyle f(x)=\cos x \) \( \displaystyle f(x)=\cos x \)
としたいのなら
=\cos x_k&chco=aa4422) \( \displaystyle f(x_k)=\cos x_k \) \( \displaystyle f(x_k)=\cos x_k \)
 \( \displaystyle x_k=\frac{\pi}{3n}k \) \( \displaystyle x_k=\frac{\pi}{3n}k \)
とすることになり
 \( \displaystyle x_0=\frac{\pi}{3n}\times 0=0,\hspace{5px}x_n=\frac{\pi}{3n}\times n=\frac{\pi}{3} \) \( \displaystyle x_0=\frac{\pi}{3n}\times 0=0,\hspace{5px}x_n=\frac{\pi}{3n}\times n=\frac{\pi}{3} \)
から,区間の幅が
 \( \displaystyle \frac{\pi}{3} \) \( \displaystyle \frac{\pi}{3} \)
になる.そのn等分として \( \displaystyle \Delta x=\frac{\pi}{3}\cdot\frac{1}{n} \)を使うことになるから \( \displaystyle \Delta x=\frac{\pi}{3}\cdot\frac{1}{n} \)を使うことになるから
\frac{1}{n}=\lim_{n\rightarrow \infty}\sum_{k=1}^n\Bigl(\frac{3}{\pi}\cos\frac{k\pi}{3n}\Bigr)\frac{\pi}{3n}\]&chs=300x45&chco=aa4422) \( \displaystyle \lim_{n\rightarrow \infty}\sum_{k=1}^n\Bigl(\cos\frac{k\pi}{3n}\Bigr)\frac{1}{n}=\lim_{n\rightarrow \infty}\sum_{k=1}^n\Bigl(\frac{3}{\pi}\cos\frac{k\pi}{3n}\Bigr)\frac{\pi}{3n} \) \( \displaystyle \lim_{n\rightarrow \infty}\sum_{k=1}^n\Bigl(\cos\frac{k\pi}{3n}\Bigr)\frac{1}{n}=\lim_{n\rightarrow \infty}\sum_{k=1}^n\Bigl(\frac{3}{\pi}\cos\frac{k\pi}{3n}\Bigr)\frac{\pi}{3n} \)
 \( \displaystyle =\frac{3}{\pi}\int_0^{\frac{\pi}{3}}\cos xdx=\frac{3}{\pi}\Bigl[\sin x\Bigr]_0^{\frac{\pi}{3}} \) \( \displaystyle =\frac{3}{\pi}\int_0^{\frac{\pi}{3}}\cos xdx=\frac{3}{\pi}\Bigl[\sin x\Bigr]_0^{\frac{\pi}{3}} \)
=\frac{3\sqrt{3}}{2\pi}&chco=aa4422) \( \displaystyle =\frac{3}{\pi}(\sin\frac{\pi}{3}-\sin 0)=\frac{3\sqrt{3}}{2\pi} \) \( \displaystyle =\frac{3}{\pi}(\sin\frac{\pi}{3}-\sin 0)=\frac{3\sqrt{3}}{2\pi} \)
【問題1】
 \( \displaystyle \lim_{n\rightarrow \infty}\frac{1}{n}\sum_{k=1}^n\sqrt{1+\frac{8k}{n}}= \) \( \displaystyle \lim_{n\rightarrow \infty}\frac{1}{n}\sum_{k=1}^n\sqrt{1+\frac{8k}{n}}= \)
(日本大2005年度)
参考答案を見る
|