|
��Excel���g������ϕ��̌v�Z
��v�_��
�y��P�z���@�s��ϕ������߂�v�Z�́C�������ƂȂ�̂ɑ��āC�ϕ���Ԃ̉��[�Ə�[���萔�ł���悤�Ȓ�ϕ��̌v�Z�́C�����萔�ƂȂ�̂�Excel�Ȃǂ̃R���s���[�^�\�t�g���g���ĊȒP�ɋ��߂邱�Ƃ��ł��܂��D ���@�敪���ϖ@�Ƃ�����ϕ��̒�`�ɂ����Ă͏���Ԃ̕����O�ɋ߂Â���Ɍ����l����̂ɑ��āC�����ŋ��߂���@�ł́u�������������ȗL���̕��v���g���ċߎ��l�����߂܂��D ���@���Z���w�ł͕����⍪����p���������Ȓl���D�܂�܂����C�����ŋ��߂���@�͏����ŕ\�����ߎ��l�ɂȂ�܂��D
���퐶���ł͗L�������R���C���R�Ȋw�v�Z�ł��L�������U��������Ώ\���ł��D
���@���̕��@�͐��l�ϕ��@�ƌĂ�C
e−x2dx��dx�̂悤�ȕM�Z�ŋ��߂��Ȃ���ϕ������߂�̂Ɏg�����Ƃ��ł��܂��D�ɒ[�Ɍ����i�L���m��l�ƂȂ���̂Ȃ�j�ǂ�Ȓ�ϕ��ł����߂邱�Ƃ��ł��܂��D �@�E�̕\�P�́C��ϕ�(−x2+3x−2)dx�̒l�����߂�菇�����������̂ł��D (1) �`���x�̒l���������݂܂��D
�@�ϕ���Ԃ̉��[1���������݁C�u�t�B���v���u�A���f�[�^�̍쐬�v���g����0.05��������悤�ɂ��܂��D
�@�����ł́u�������������ȗL���̕��v�Ƃ���0.05�Ƃ��܂����D�����1����2�܂ł�20��������Ƃ������Ƃł��D���̒l�́C�b��ɏ������ށu�����`�̉����v�Ɏg���܂��D
(2) �E�}�P�̂悤�ɂ��ꂼ��̒����`�̏c�̒����Ɖ��̒������|���Ėʐς����߁C�S�̂̍��v�����߂邱�Ƃ��l���܂��D�@���x�̍����l���K�v�ȂƂ��͕������ׂ�������ł��܂����Excel���[�N�V�[�g�ł�10000�����ł��ł��܂����C���ۏ�悭�g��������3�ʒ��x�̐��l�Ȃ�100�������炢�ŏ\�����߂��܂��D �@���̂��߂ɁC�܂��a��ɏc�̒���y=f(x)=−x2+3x−2�̒l���v�Z���鎮�����܂��D
�@B2�̃Z���� =-(A2^2-3*A2+2) �Ə������݁C���̎����R�s�[���Ăa��̎c��̃Z���ɓ\��t���܂��D
(3) ���Ɋe�����`�̉��̒������b��ɏ������݂܂��D
�@�`���x�̒l��0.05�����₵�Ă���̂ŁC�e�����`�̉��̒����͂��ׂ�0.05�ɂȂ�܂��D
(4) �a��̒l�Ƃb��̒l���|����Ɗe�����`�̖ʐς����܂�܂��D
�@D2�̃Z���� =B2*C2 �Ə������݁C���̎����R�s�[���Ăc��̎c��̃Z���ɂ��\��t���܂��D
(5) �c��̒l�̘a�����߂܂��D
�@D23�� =SUM(D2:D21) �Ə������ނƏo���オ��D
�@D22�̃Z���͑����Ȃ����Ƃɒ���
����Ŏ��������@�ł́C�e�����`�̍���[���Ȑ��Ɛڂ����`�Œ����`�����̂ŁC�\�P�̓��F�̔w�i�F�Ŏ������������C�}�P�̓��F�Ŏ����������`�̖ʐς̌v�Z�ɂȂ��Ă���D
�@�}�P���番����悤�ɁC���̂悤�ɋߎ�����ƋȐ������������ԁi�}�ł�0��x��1.50�̋�ԁj�ɂ����Ē����`�̖ʐς́C�^�̖ʐς������������Ȃ��D�t�ɋȐ������������ԁi�}�ł�1.50��x��2.00�̋�ԁj�ɂ����Ē����`�̖ʐς́C�^�̖ʐς��������������D �@�敪���ϖ@�ł́C����������Ȃ��ׂ�������Ɍ����l����̂ł����̌덷���O�ɂȂ��Đ^�̖ʐςɎ������邪�C��L�̂悤�Ȑ��l�ϕ��ł͋��߂鐔�l�̐��x�ɉ����ĕ����̎d�����l����Ƃ悭�C�����Ŏ������悤�ȑ����̋�Ԃ������̋�Ԃ�����悤�Ȋ��ł͑��E�����20�������x�ŏ\���悢�ߎ��l��������D ��Excel�ŏ�L�̂悤�ȕ\��g�ݗ��ĂĂ����ƁC�E�}�Q�̂悤�ȃO���t���ȒP�ɕ`����D�i�\�P�ɂ�����A2:B21�͈̔͂�I�����āC�O���t���U�z�}�i�������t���j��I�ԂƂ悢���x���W���͈͓��Ɋ܂߂�Ƃ����܂���O���t�ł͂Ȃ��D�j |
�\�P
�}�P 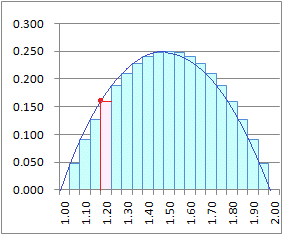
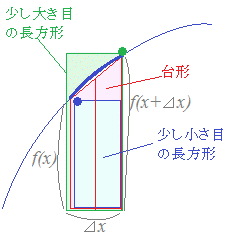
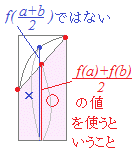
�����l�ϕ��ɂ��Ă͌�Z�͈̔͂����߂����������܂��������ł͈����܂���D �@���}�R�̂悤�ɏ����傫�߂Ɏ���������`�i�����̋�Ԃł͉E�[�̒l���c�̒����ɂ���C�����̋�Ԃł͍��[�̒l���c�̒����ɂ���j�Ə��������߂Ɏ���������`�i���L�̋t�j�Ƃ��L�����������܂ň�v����C���̗L�������܂ł͐��m�Ȓl�ƍl���邱�Ƃ��ł��C����炪�������̂Ƃ��Ɋ��S�Ɉ�v������̋Ɍ��l���ʐς̒�`���ƍl���邱�Ƃ��ł��܂��D |