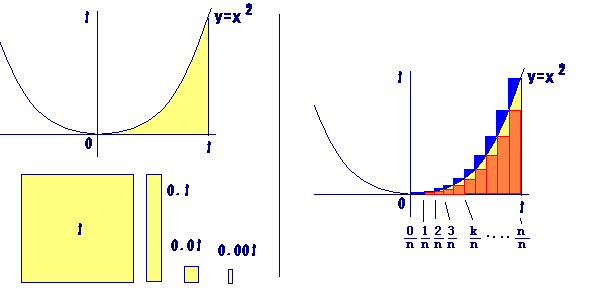
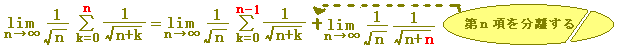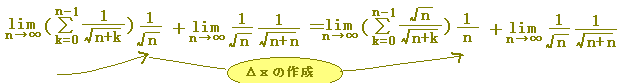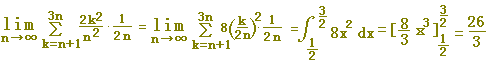■ 以上により,S=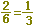 ・・・これが,求める図形の面積です. ・・・これが,求める図形の面積です.
■ 定積分との関係
上の図形の面積は,定積分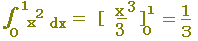 で表わされます. で表わされます.
これらを比較すると,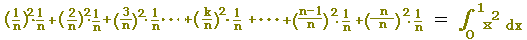
すなわち,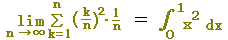
上組と下組は等しいので,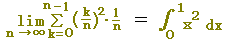 も成立します. も成立します.
数列の和の極限を定積分に直す方法
■ 数列の和の極限を定積分に直すには,次のような図を考えます.
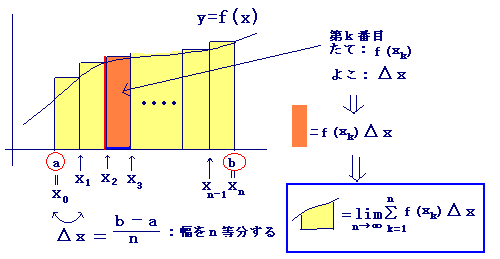
(公式)
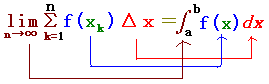
|
■ この公式を使うには,「各部品」を正確に対応させることが大切です.(初めは,大変難しいものです.)
<要点>
1 まず,Δx(通常は1/n)を分離すること:これがdxになります.
(Σ記号の初項から末項までの項数n個の等分となっている)
2 xkを決める → f(xk)を決める → f(x)を決める.
3 limΣ→∫ とします.
4 x0=a,xn=b とします.(b-a=1でないなら,1の段階でΔxを調整します.)
(例1) 次の極限値を定積分に直し,その値を求めなさい.【ポイント:Δxの役割】
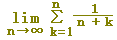
(考え方)
-
1/n=Δx がなければ積分できません.なければ作ります.このために,1/nでくくります.(区間の幅は1)
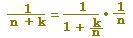
-
k/n=xk → f(xk)=
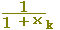 → f(x)= → f(x)=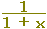 とします. とします.
-
k/n=xk → a=x0=0, b=xn=1(区間の幅は1でよい.)
-
limΣを∫にします.
(答案)
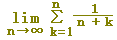 = =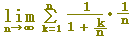 = =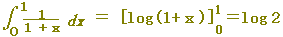
(例2) 次の極限値を定積分に直し,その値を求めなさい.【ポイント:区間の幅】
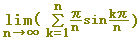
(考え方1)
-
1/nでくくります.(区間の幅は1)
-
xk=k/n → f(xk)=πsinπxk
→ f(x)=πsinπx
-
xk=k/n →a=x0=0,b=xn=1
(区間の幅は1)
-
limΣを∫にします.
|
(考え方2)
-
π/n=Δxとします.(区間の幅はπ)
-
xk=kπ/n → f(xk)=sinxk
→ f(x)=sinx
-
xk=kπ/n →a=x0=0,b=xn=π
(区間の幅はπ)
-
limΣを∫にします.
|
(例3) 次の極限値を定積分に直し,その値を求めなさい.【ポイント:xk←→f(xk)←→f(x)】
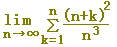
(考え方1)
-
1/nでくくります.(区間の幅は1)
-
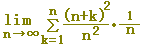 = =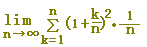
-
xk=k/nとおくと, f(xk)=(1+xk)2
f(x)=(1+x)2
-
a=x0=0, b=xn=1(区間の幅は1)
-
limΣを∫にします.
|
(考え方2)
-
1/nでくくります.(区間の幅は1)
-
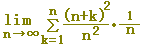 = =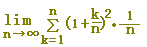
-
xk=1+k/nとおくと, f(xk)=xk2
f(x)=x2
-
a=x0=1, b=xn=2(区間の幅は1)
-
limΣを∫にします.
|
(例4) 次の極限値を定積分に直し,その値を求めなさい.【ポイント:皮1枚過剰→引いてから足す】
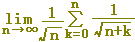
(考え方)
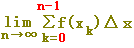 または または 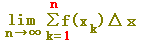 が が 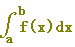 に等しいので, に等しいので,
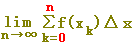 では,「皮1枚分」多いことになります.(次の図参照) では,「皮1枚分」多いことになります.(次の図参照)
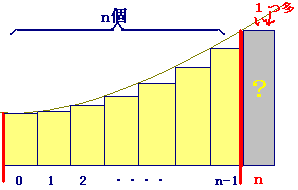 → →
この場合,「大した違いはないから」などとあいまいにせず,「過剰分を引いて定積分を完成してから」「右端(または左端)の項を加え」ます.
(答案)
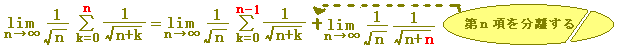
=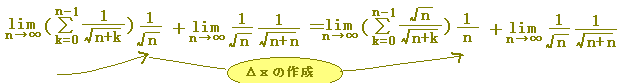
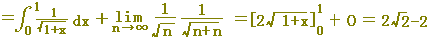
(例5) 次の極限値を定積分に直し,その値を求めなさい.【ポイント:皮1枚不足→足してから引く】
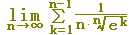
(考え方)
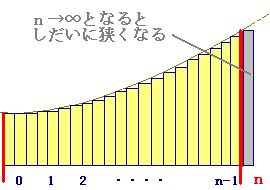
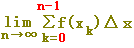 または または 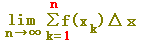 が が 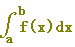 に等しいので,この問題では「皮1枚分不足」です. に等しいので,この問題では「皮1枚分不足」です.
この場合,「不足分を埋めて,定積分を完成してから」「引きます」.(次の図参照)(埋めるのは,左端でもよい.)
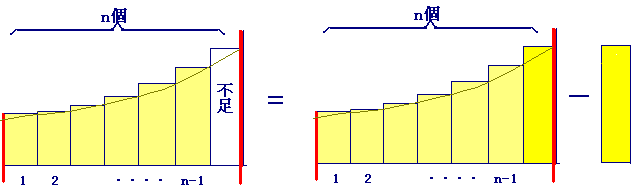
(答案)
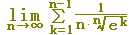 = =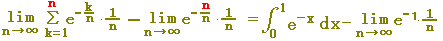
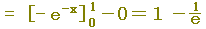
(例6) 次の極限値を定積分に直し,その値を求めなさい.【ポイント:3n等分→Δx=1/(3n)】
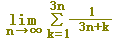
(考え方)
k=1~3nなので,短冊の横幅としてΔx=1/(3n)を使うと,図形を想像しやすくなります.
(答案)
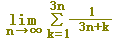 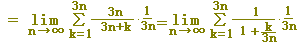
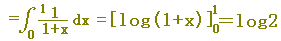
※ (例1)でnに3nを代入したものと一致します.
(例7) 次の極限値を定積分に直し,その値を求めなさい.【ポイント:a→初項,b→末項】
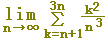
(考え方)
k=n+1~3n なので,項数は2nです.
Δx=1/(2n),xk=k/(2n)とおくとき,a=xn=1/2,b=x3n=3/2 です.
(答案)
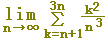
=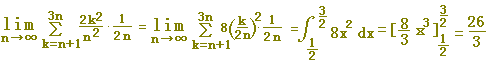
《問題》
次の極限値を定積分に直したとき,右欄のどの式と等しくなりますか.
|

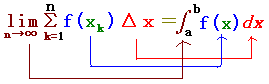
 →
→