【体積を求める積分計算】
多項式形の積分で数学Ⅱの範囲で求められる体積の問題は, 別のページにあります.
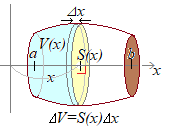 (1)
(1) 一般の立体の体積
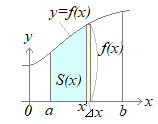
x軸に垂直な平面で立体を切ったときの断面積が ) \( \displaystyle S(x) \) \( \displaystyle S(x) \)のとき,この立体の体積Vは
dx\]&chco=0000ff) \( \displaystyle V=\int_a^bS(x)dx \) \( \displaystyle V=\int_a^bS(x)dx \)
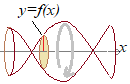
(2) 曲線 ) \( \displaystyle y=f(x) \) \( \displaystyle y=f(x) \),2直線 ) \( \displaystyle x=a,\hspace{3px}x=b\hspace{13px}(a\lt b) \) \( \displaystyle x=a,\hspace{3px}x=b\hspace{13px}(a\lt b) \)で囲まれた図形を  \( \displaystyle x \) \( \displaystyle x \)軸のまわりに回転させてできる回転体の体積
\}^2dx\]&chco=0000ff) \( \displaystyle V=\pi\int_a^b\{f(x)\}^2dx \) \( \displaystyle V=\pi\int_a^b\{f(x)\}^2dx \)
 \( \displaystyle x \) \( \displaystyle x \)軸に垂直な断面は円になり,その半径が &chco=aa4422) \( \displaystyle f(x) \) \( \displaystyle f(x) \)であるから断面積は =\pi\{f(x)\}^2&chco=aa4422) \( \displaystyle S(x)=\pi\{f(x)\}^2 \) \( \displaystyle S(x)=\pi\{f(x)\}^2 \)になる.
&chco=aa4422) \( \displaystyle f(x) \) \( \displaystyle f(x) \)は負の値も取り得るから正確には \mid&chco=aa4422) \( \displaystyle \mid f(x)\mid \) \( \displaystyle \mid f(x)\mid \)というべきだが,2乗するので結果は同じになる.また,図のように &chco=aa4422) \( \displaystyle y=f(x) \) \( \displaystyle y=f(x) \)のグラフが  \( \displaystyle x \) \( \displaystyle x \)軸を横切っていても構わない.
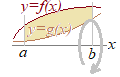
(3) 2曲線 ,\hspace{3}y=g(x)) \( \displaystyle y=f(x),\hspace{3px}y=g(x) \) \( \displaystyle y=f(x),\hspace{3px}y=g(x) \),2直線 ) \( \displaystyle x=a,\hspace{3px}x=b\hspace{13px}(a\lt b) \) \( \displaystyle x=a,\hspace{3px}x=b\hspace{13px}(a\lt b) \)で囲まれた図形を  \( \displaystyle x \) \( \displaystyle x \)軸のまわりに回転させてできる回転体の体積(ただし,  \( \displaystyle a\leqq x\leqq b \) \( \displaystyle a\leqq x\leqq b \)において, \underline{\ge}g(x)\underline{\ge}0) \( \displaystyle f(x)\geqq g(x)\geqq 0 \) \( \displaystyle f(x)\geqq g(x)\geqq 0 \)とする)
\}^2-\{g(x)\}^2\right]dx\]&chco=0000ff) \( \displaystyle V=\pi\int_a^b\left[\{f(x)\}^2-\{g(x)\}^2\right]dx \) \( \displaystyle V=\pi\int_a^b\left[\{f(x)\}^2-\{g(x)\}^2\right]dx \)
ちくわのような中抜きの筒の体積を求めるには,外側の円の面積 \}^2&chco=aa4422) \( \displaystyle \pi\{f(x)\}^2 \) \( \displaystyle \pi\{f(x)\}^2 \)から内側の円の面積 \}^2&chco=aa4422) \( \displaystyle \pi\{g(x)\}^2 \) \( \displaystyle \pi\{g(x)\}^2 \)を引いたものが断面積だと考えるとよい.
間違っても, -g(x)\}^2&chco=aa4422) \( \displaystyle \pi\{f(x)-g(x)\}^2 \) \( \displaystyle \pi\{f(x)-g(x)\}^2 \)などとしてはいけない!
|
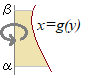 (4) 曲線
(4) 曲線) \( \displaystyle x=g(y) \),2直線 \( \displaystyle x=g(y) \),2直線) \( \displaystyle y=\alpha,\hspace{3px}y=\beta\hspace{13px}(\alpha\lt\beta) \)で囲まれた図形を \( \displaystyle y=\alpha,\hspace{3px}y=\beta\hspace{13px}(\alpha\lt\beta) \)で囲まれた図形を \( \displaystyle y \)軸のまわりに回転させてできる回転体の体積 \( \displaystyle y \)軸のまわりに回転させてできる回転体の体積
\}^2dy\]&chco=0000ff) \( \displaystyle V=\pi\int_{\alpha}^{\beta}\{g(y)\}^2dy \) \( \displaystyle V=\pi\int_{\alpha}^{\beta}\{g(y)\}^2dy \)
(2)のx軸とy軸の立場を入れ換えたものになるから,y軸に垂直な断面の半径は &chco=aa4422) \( \displaystyle x=g(y) \) \( \displaystyle x=g(y) \)になる
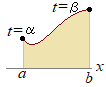
(5) 媒介変数表示 ,\hspace{2}y=g(t)) \( \displaystyle x=f(t),\hspace{2px}y=g(t) \) \( \displaystyle x=f(t),\hspace{2px}y=g(t) \)で表される曲線で, ,\hspace{3}b=f(\beta)) \( \displaystyle a=f(\alpha),\hspace{3px}b=f(\beta) \) \( \displaystyle a=f(\alpha),\hspace{3px}b=f(\beta) \)のとき,  \( \displaystyle a\leqq x\leqq b \) \( \displaystyle a\leqq x\leqq b \)で囲まれる図形を  \( \displaystyle x \) \( \displaystyle x \)軸のまわりに回転させてできる回転体の体積
\}^2f\apos(t)dt\]&chco=0000ff) \( \displaystyle V=\pi\int_a^by^2dx=\pi\int_{\alpha}^{\beta}\{g(t)\}^2f'(t)dt \) \( \displaystyle V=\pi\int_a^by^2dx=\pi\int_{\alpha}^{\beta}\{g(t)\}^2f'(t)dt \)
&chco=aa4422) \( \displaystyle \frac{dx}{dt}=f'(t) \) \( \displaystyle \frac{dx}{dt}=f'(t) \)により, dt&chco=aa4422) \( \displaystyle dx=f'(t)dt \) \( \displaystyle dx=f'(t)dt \)を代入する
|
 (面積の復習)
(面積の復習) (体積の計算)
(体積の計算) (2) 曲線
(2) 曲線 (3) 2曲線
(3) 2曲線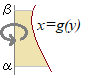 (4) 曲線
(4) 曲線 (5) 媒介変数表示
(5) 媒介変数表示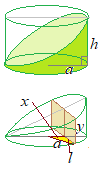 【例題1.1】
【例題1.1】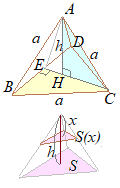
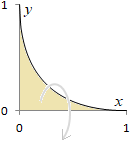
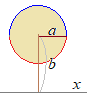 (解答)
(解答)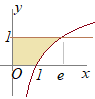 (解答)
(解答)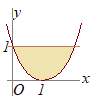 (解答)
(解答)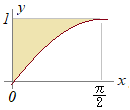 (解答)
(解答)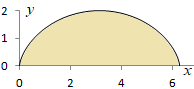
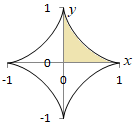
 (解説)
(解説)