|
پ،•آ‹بگü‚إˆح‚ـ‚ꂽگ}Œ`‚ج–تگد‚R…پi”}‰î•دگ”•\ژ¦پj
پy—ل‚Pپz
پi‰ً“ڑپjپ@a>0, b>0, 0پ…tپ…2ƒخ‚ج‚ئ‚«پCx=acost , y=bsint‚إˆح‚ـ‚ꂽگ}Œ`‚ج–تگد‚ً‹پ‚ك‚ؤ‚‚¾‚³‚¢پD پm‹بگü‚جٹTŒ`‚ً•`‚پn (1) t‚ج•د‰»‚ة‘خ‰‚µ‚½x, y‚ج‘Œ¸‚ً’²‚ׂéپD
=−asint, =bcost‚¾‚©‚ç
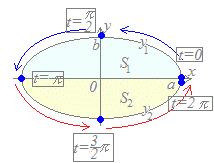 (2) پm y dx‚جŒ`‚إ–تگد‚ً•\‚·پn گآ‚إژ¦‚µ‚½•”•ھ‚ج–تگد‚ح y1 dx ƒsƒ“ƒN‚إژ¦‚µ‚½•”•ھ‚ج–تگد‚ح (−y2)dx ‹پ‚ك‚éگ}Œ`‚ج–تگد‚ح S=y1 dx−(−y2 )dx (3) پm ’uٹ·گد•ھ‚ة‚و‚è•دگ”‚ًt‚ة’¼‚µ‚ؤŒvژZ‚·‚éپn پi”يگد•ھٹضگ”پjپ@پFپ@y → bsint پiگد•ھ•دگ”پjپ@پFپ@dx=−asintdt پiگد•ھ‹وٹشپjپ@پFپ@
‘±‚پ¨
|
پiژQچl‚Pپj
پ@چ¶‚ج•û’ِژ®‚حپC‘ب‰~ +=1 ‚ج”}‰î•دگ”•\ژ¦‚ة‚ب‚ء‚ؤ‚¢‚ـ‚·پD
پiژQچl‚Qپj
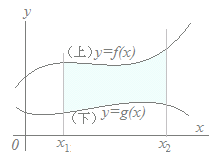 پ@‚ئ‚¢‚¤‚ج‚حپC‚±‚ج–â‘è‚إ‚حپiڈمپj‚ئپi‰؛پj‚حٹضگ”Œ`‚ة‚و‚ء‚ؤ‹و•ت‚³‚ê‚é‚ج‚إ‚ح‚ب‚پCپiڈمپjپi‰؛پj‚جٹضگ”Œ`‚ح“¯‚¶‚ة‚ب‚邽‚كپC’Pڈƒ‚ةˆّ‚«ژZ‚ً‚·‚ê‚خڈء‚¦‚ؤ‚ب‚‚ب‚ء‚ؤ‚µ‚ـ‚¢‚ـ‚·پD پ@پiڈمپj‚إ‚ ‚é‚©پi‰؛پj‚إ‚ ‚é‚©‚حt‚جگد•ھ‹وٹش‚ة‚و‚ء‚ؤ‹و•ت‚³‚ê‚ؤ‚¢‚ـ‚·پD‚¾‚©‚çپCچ¶گ}‚ج‚و‚¤‚ةxژ²‚ئ‚إˆح‚ـ‚ê‚éگ}Œ`‚ج–تگد‚ً‚Q‚آ‚ة•ھ‚¯‚ؤŒvژZ‚µ‚ـ‚·پD پ¨‘±‚« S=bsint(−asint)dt−bsint(−asint)dt =−absin2dt+absin2dt =absin2dt+absin2dt =absin2dt =abdt =ab−=ƒخab
a=b(=r)‚ج‚ئ‚«‚حپC‰~‚ة‚ب‚è,S=ƒخr2‚ئ‚ب‚è‚ـ‚·پD
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
پy—ل‚Qپz
پi‰ً“ڑپjپ@a>0‚ج‚ئ‚«پCx=a(t−sint) , y=a(1−cost)‚ئxژ²‚ئ‚إˆح‚ـ‚ꂽگ}Œ`‚ج–تگد‚ً‹پ‚ك‚ؤ‚‚¾‚³‚¢پD پm‹بگü‚جٹTŒ`‚ً•`‚پn (1) t‚ج•د‰»‚ة‘خ‰‚µ‚½x, y‚ج‘Œ¸‚ً’²‚ׂéپD
=a(1−cost)پ†0, =asint‚¾‚©‚ç
(2) پm y dx‚جŒ`‚إ–تگد‚ً•\‚·پn S=y dx (3) پm ’uٹ·گد•ھ‚ة‚و‚è•دگ”‚ًt‚ة’¼‚µ‚ؤŒvژZ‚·‚éپn پi”يگد•ھٹضگ”پjپ@پFپ@y → a(1−cost) پiگد•ھ•دگ”پjپ@پFپ@dx=a(1−cost)dt پiگد•ھ‹وٹشپjپ@پFپ@
‘±‚پ¨
|
پiژQچl‚Rپj
پ@چ¶‚جƒOƒ‰ƒt‚حƒTƒCƒNƒچƒCƒh‚ئŒؤ‚خ‚êپC‰~‚ھ’¼گüڈم‚ًٹٹ‚炸‚ة‰ٌ“]‚·‚é‚ئ‚«‚ةپC‰~ژüڈم‚ج‚P“_‚ھ•`‚‹Oگص‚ئ‚ب‚ء‚ؤ‚¢‚ـ‚·پD 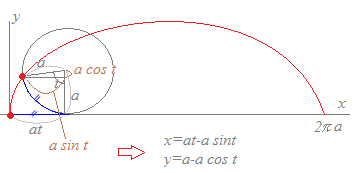 پ¨‘±‚« S=a(1−cost)·a(1−cost)dt =a2(1−2cost+cos2t)dt =a2(1−2cost+)dt =a2t−2sint+=3ƒخa2 پ@–تگد‚ھ‰~‚ج‚؟‚ه‚¤‚ا‚R”{S=3·ƒخa2‚ة‚ب‚é‚ج‚حپC‹»–،گ[‚¢‚±‚ئ‚إ‚·پD 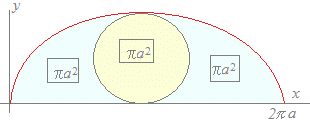 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
پy–â‘è‚Pپzژں‚ج“r’†ŒvژZ‚ًژQچl‚ة‚µ‚ؤx=sint , y=sin2t(0پ…tپ…ƒخ)‚إˆح‚ـ‚ê‚éگ}Œ`‚ج–تگد‚ً‹پ‚ك‚ؤ‚‚¾‚³‚¢
HELPپi“r’†ŒvژZپj =cost , =0 پج t= =2cos2t , =0 پج t=,
ƒOƒ‰ƒt‚حژں‚ج‚و‚¤‚ة‚ب‚éپD 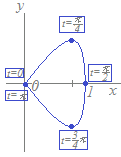 |
ژOٹpٹضگ”‚جŒِژ®‚ًژg‚ء‚ؤپCگد‚ًکa‚ة’¼‚µ‚ؤ‚©‚çگد•ھ‚µ‚ـ‚·پD S=sin2tcost dt ={ sin3t+sint }dt =−−cost ={ (+1)−(−−1) }= | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
پy–â‘è‚Qپzژں‚ج“r’†ŒvژZ‚ًژQچl‚ة‚µ‚ؤx=sin2t , y=sin3t(0پ…tپ…)‚إˆح‚ـ‚ê‚éگ}Œ`‚ج–تگد‚ً‹پ‚ك‚ؤ‚‚¾‚³‚¢
HELPپiپ¦ˆأژZ‚إ‚ح‚إ‚«‚ـ‚¹‚ٌپDŒvژZ—pژ†‚ھ•K—v‚إ‚·پDپj پi“r’†ŒvژZپj =2cos2t , =0 پج 2t= پج t= =3cos3t , =0 پج 3t= پج t= y=0 پج 3t=0,ƒخ پج t=0,
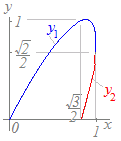 |
S=y1 dx−y2 dx =sin3t·2cos2t dt−sin3t·2cos2t dt =sin3t·2cos2t dt+sin3t·2cos2t dt =sin3t·2cos2t dt ژOٹpٹضگ”‚جŒِژ®‚ًژg‚ء‚ؤپCگد‚ًکa‚ة’¼‚µ‚ؤ‚©‚çگد•ھ‚µ‚ـ‚·پD S=(sin5t+sint)dt =−−cost ={ (−−)−(−−1) }== | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
پy–â‘è‚Rپzx=t2 , y=t3−3t‚إˆح‚ـ‚ê‚éگ}Œ`‚ج–تگد‚ً‹پ‚ك‚ؤ‚‚¾‚³‚¢
HELPپiپ¦ˆأژZ‚إ‚ح‚إ‚«‚ـ‚¹‚ٌپDŒvژZ—pژ†‚ھ•K—v‚إ‚·پD‘¬‚¢گl‚إ‚à10•ھ‚ح‚©‚©‚é‚إ‚µ‚ه‚¤پDپj =2t , =0 پج t=0 =3t2−3t , =0 پج t=±1 y=0 پج t(t2−3)=0 پج t=0,±
|
ƒOƒ‰ƒt‚حژں‚ج‚و‚¤‚ة‚ب‚éپD
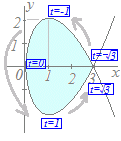 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||